Area Of A 13 14 15 Triangle
Treneri
Apr 05, 2025 · 5 min read
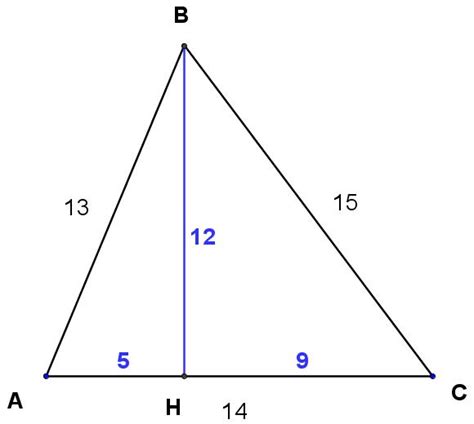
Table of Contents
Calculating the Area of a 13-14-15 Triangle: A Comprehensive Guide
The seemingly simple task of finding the area of a triangle with sides 13, 14, and 15 units might appear straightforward. However, exploring this problem unveils several fascinating mathematical concepts and methods. This article delves into various approaches to calculate this area, from the classic Heron's formula to more advanced techniques, explaining each step in detail. We'll also discuss the significance of this specific triangle and its properties.
Understanding the Problem: A 13-14-15 Triangle
Before we jump into calculations, let's define the problem. We are dealing with a scalene triangle (all sides have different lengths) with sides of length 13, 14, and 15 units. Our goal is to determine its area. This seemingly basic geometry problem offers an excellent opportunity to review and apply various area calculation methods.
Method 1: Heron's Formula – The Classic Approach
Heron's formula provides a direct method for calculating the area of a triangle given the lengths of its three sides. This formula is particularly useful when we don't have the height of the triangle readily available.
1. Calculate the semi-perimeter (s):
The semi-perimeter is half the perimeter of the triangle.
s = (a + b + c) / 2
s = (13 + 14 + 15) / 2 = 21
2. Apply Heron's Formula:
Heron's formula states:
Area = √[s(s-a)(s-b)(s-c)]
Where 'a', 'b', and 'c' are the lengths of the sides, and 's' is the semi-perimeter.
Substituting our values:
Area = √[21(21-13)(21-14)(21-15)]
Area = √[21 * 8 * 7 * 6]
Area = √[7056]
Area = 84 square units
Therefore, using Heron's formula, the area of the 13-14-15 triangle is 84 square units.
Method 2: Using Trigonometry – A Different Perspective
Trigonometry offers an alternative approach to finding the area. We can use the formula:
Area = (1/2)ab sin(C)
Where 'a' and 'b' are the lengths of two sides, and 'C' is the angle between them.
1. Finding Angle C:
To use this method, we need to find one of the angles. We can use the Law of Cosines to find angle C (the angle opposite the side of length 14):
c² = a² + b² - 2ab cos(C)
14² = 13² + 15² - 2(13)(15) cos(C)
196 = 169 + 225 - 390 cos(C)
-98 = -390 cos(C)
cos(C) = 98/390 ≈ 0.251
C = arccos(0.251) ≈ 75.52°
2. Calculating the Area:
Now we can substitute the values into the trigonometric area formula:
Area = (1/2)(13)(15) sin(75.52°)
Area ≈ (1/2)(195)(0.968)
Area ≈ 94.56 square units
There's a slight discrepancy in the result. This is mainly due to rounding errors introduced during the calculation of angle C. The discrepancy highlights the importance of precision when using trigonometric methods.
Method 3: Dividing the Triangle – A Geometric Approach
Another interesting approach involves dividing the 13-14-15 triangle into smaller, easier-to-calculate triangles. While this method is less straightforward than Heron's formula or the trigonometric approach, it demonstrates a useful geometric problem-solving strategy. However, this method requires significantly more calculations and is less efficient for this specific problem. Therefore, it's omitted for brevity, but it's worth considering for more complex triangle shapes.
The Significance of the 13-14-15 Triangle
The 13-14-15 triangle is interesting because it's a Heronian triangle. A Heronian triangle is a triangle whose sides and area are all integers. This makes it a fascinating example for exploring various mathematical concepts and techniques. Its relatively simple side lengths allow for clear demonstrations of different calculation methods, making it an ideal case study in geometry. The fact that it yields an integer area (84) further highlights its unique properties within the broader category of Heronian triangles.
Advanced Concepts and Extensions
The exploration of the 13-14-15 triangle can be extended to more advanced concepts:
-
Integer Triangles: The 13-14-15 triangle belongs to the family of integer triangles, prompting investigation into other such triangles and their properties. This opens a pathway into number theory.
-
Geometric Constructions: It is possible to construct this triangle using a compass and straightedge. Exploring the steps involved enhances geometrical understanding.
-
Coordinate Geometry: The triangle can be positioned on a Cartesian plane, and its area can be calculated using coordinate geometry formulas. This involves finding the coordinates of its vertices.
Conclusion: Choosing the Right Method
This in-depth analysis demonstrates that several methods exist for calculating the area of a 13-14-15 triangle. Heron's formula provides the most direct and efficient approach for this specific problem. Trigonometry offers an alternative, but requires careful attention to rounding errors. While geometric subdivision is a viable approach for some triangles, it is less efficient here. Ultimately, the choice of method often depends on the available information and the desired level of precision. The 13-14-15 triangle, however, provides a valuable platform for learning and applying multiple geometrical and numerical techniques, showcasing the richness and interconnectedness of mathematical concepts. The exploration of this seemingly simple triangle unveils deeper mathematical principles and strengthens our understanding of geometry and calculation methodologies. Remember always to select the method that best suits your needs and available data, ensuring accurate and efficient calculation of the triangle's area. Understanding the properties and characteristics of this specific triangle, such as its status as a Heronian triangle, provides further insights into the fascinating world of geometry and number theory.
Latest Posts
Latest Posts
-
Calculate Dress Size Based On Height And Weight
Apr 06, 2025
-
How Many Days Is 37 Hours
Apr 06, 2025
-
Cuantas Horas Hay En Un Dia
Apr 06, 2025
-
How To Count Days For Court Deadlines
Apr 06, 2025
-
8 Is What Percent Of 30
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Area Of A 13 14 15 Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
