Find The Gcf Of 18j + 27
Treneri
May 13, 2025 · 5 min read
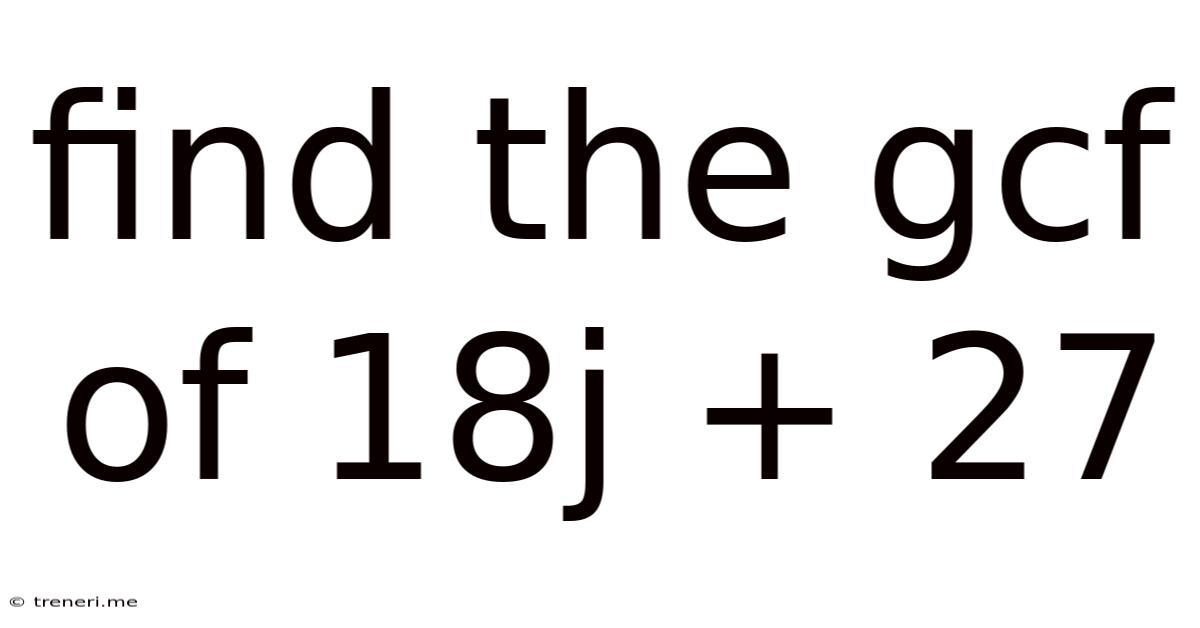
Table of Contents
Finding the Greatest Common Factor (GCF) of 18j + 27: A Comprehensive Guide
Finding the greatest common factor (GCF) is a fundamental concept in algebra and number theory. It plays a crucial role in simplifying expressions, solving equations, and understanding the relationships between numbers. This article will delve into the process of finding the GCF of the algebraic expression 18j + 27, explaining the underlying principles and providing practical examples. We'll also explore different methods and address common misconceptions.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific expression 18j + 27, let's solidify our understanding of GCFs. The greatest common factor of two or more numbers (or terms in an algebraic expression) is the largest number that divides evenly into all of them without leaving a remainder. Think of it as the largest shared factor among the numbers.
For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides evenly into both 12 and 18. (12 = 6 x 2 and 18 = 6 x 3).
When dealing with algebraic expressions like 18j + 27, we're looking for the greatest common factor of the coefficients (the numbers in front of the variables) and any common variables.
Finding the GCF of 18j + 27: Step-by-Step
Let's break down the process of finding the GCF of 18j + 27:
1. Identify the Coefficients and Variables
The expression 18j + 27 consists of two terms: 18j and 27. The coefficients are 18 and 27. The variable is 'j', but it's only present in one term.
2. Find the GCF of the Coefficients
To find the GCF of 18 and 27, we can use several methods:
-
Listing Factors: List all the factors of each number and identify the largest common factor.
Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 27: 1, 3, 9, 27
The common factors are 1, 3, and 9. The greatest common factor is 9.
-
Prime Factorization: Break down each number into its prime factors (numbers divisible only by 1 and themselves). The GCF is the product of the common prime factors raised to the lowest power.
18 = 2 x 3 x 3 = 2 x 3² 27 = 3 x 3 x 3 = 3³
The only common prime factor is 3, and the lowest power is 3¹. Therefore, the GCF is 3². This simplifies to 9.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
27 = 1 x 18 + 9 18 = 2 x 9 + 0
The last non-zero remainder is 9, so the GCF is 9.
3. Account for Variables
In our expression, the variable 'j' appears only in one term (18j). Therefore, it's not a common factor and doesn't affect the GCF of the entire expression.
4. Factor out the GCF
Now that we've determined the GCF is 9, we factor it out of the expression:
18j + 27 = 9(2j + 3)
Therefore, the greatest common factor of 18j + 27 is 9.
Applications of Finding GCFs
The ability to find the GCF is vital in various mathematical contexts:
-
Simplifying Algebraic Expressions: Factoring out the GCF simplifies expressions, making them easier to work with. This is crucial for solving equations and simplifying complex formulas. For instance, simplifying 18j + 27 to 9(2j + 3) makes further manipulations much simpler.
-
Solving Equations: GCFs often play a key role in solving equations, especially those involving factoring.
-
Working with Fractions: Finding the GCF is essential for simplifying fractions by dividing both the numerator and the denominator by their GCF.
-
Number Theory: GCFs form the basis of numerous concepts in number theory, such as finding the least common multiple (LCM) and understanding modular arithmetic.
Common Mistakes to Avoid
Several common pitfalls can arise when finding GCFs:
-
Confusing GCF with LCM: The greatest common factor (GCF) is different from the least common multiple (LCM). The GCF is the largest number that divides both numbers, while the LCM is the smallest number that is a multiple of both numbers.
-
Incorrectly Identifying Prime Factors: Make sure to identify only the prime factors of the numbers when using the prime factorization method.
-
Forgetting to Consider all Terms: When working with algebraic expressions, make sure to consider all terms when identifying common factors.
-
Not Factoring Completely: After factoring out the GCF, always double-check to ensure that the expression is fully factored.
Advanced Applications and Extensions
The concept of GCFs extends beyond simple algebraic expressions:
-
Polynomials: Finding the GCF is crucial for factoring polynomials, which is essential in solving polynomial equations and analyzing their roots. The methods discussed above can be applied, but you may need to consider the variables as well as the coefficients.
-
Multiple Variables: If you have an expression with multiple variables, you would find the GCF for each variable separately and then combine them. For example, if you have 12xy + 18x, the GCF is 6x (since 6 is the GCF of 12 and 18, and x is common to both terms).
-
Numerical Methods for Large Numbers: For extremely large numbers, efficient numerical algorithms like the Euclidean algorithm become essential for quickly finding the GCF.
Conclusion: Mastering GCFs for Algebraic Success
Mastering the concept of the greatest common factor is fundamental to success in algebra and related mathematical fields. By understanding the different methods for finding the GCF – listing factors, prime factorization, and the Euclidean algorithm – and by avoiding common mistakes, you can confidently tackle even the most complex algebraic expressions. Remember, the ability to find the GCF is not just a procedural skill; it's a key to unlocking deeper understanding and proficiency in mathematics. The example of finding the GCF of 18j + 27, while seemingly simple, illustrates a concept with broad applications and significance in various areas of mathematics. The ability to efficiently and accurately calculate GCFs is essential for continued progress in mathematical studies.
Latest Posts
Latest Posts
-
Round 46 To The Nearest Ten
May 13, 2025
-
How Many Grams Are In 1 Oz Of Silver
May 13, 2025
-
What Is The Reciprocal Of 4 7
May 13, 2025
-
Born In 56 How Old Am I
May 13, 2025
-
Cuanto Es 30 Libras En Kilogramos
May 13, 2025
Related Post
Thank you for visiting our website which covers about Find The Gcf Of 18j + 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.