Find The Unit Rate. 180 Miles In 3 Hours
Treneri
May 14, 2025 · 5 min read
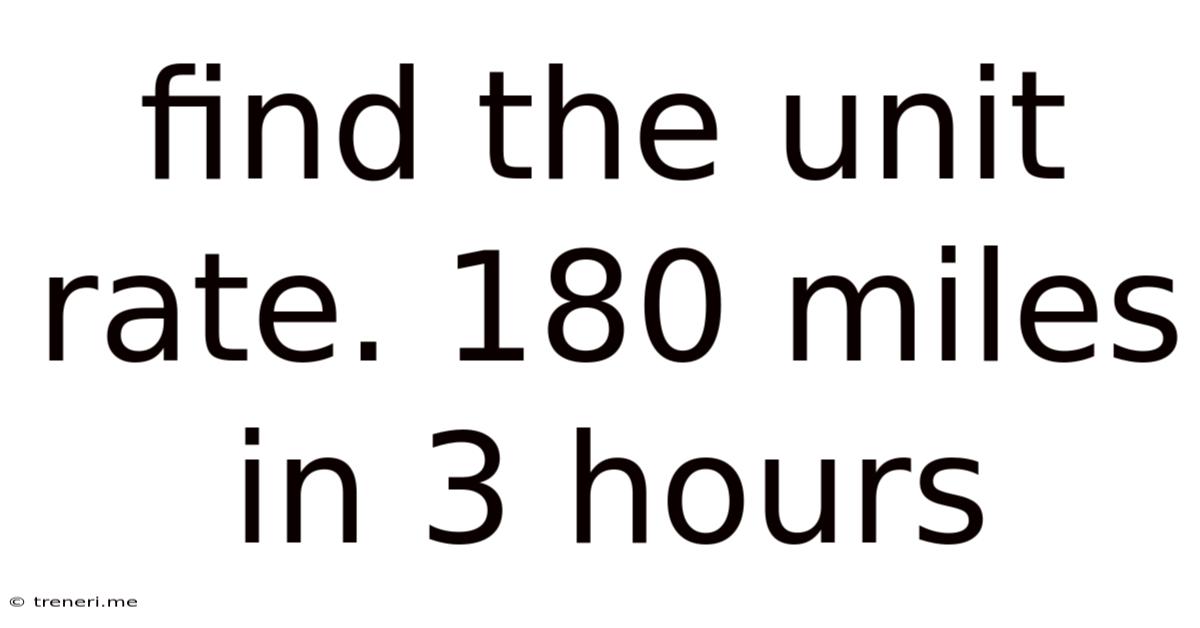
Table of Contents
Finding the Unit Rate: Mastering Miles Per Hour and Beyond
Finding the unit rate is a fundamental concept in mathematics with wide-ranging applications in everyday life. Understanding how to calculate unit rates allows you to compare prices, speeds, and various other quantities effectively. This comprehensive guide will walk you through the process of finding unit rates, using the example of 180 miles in 3 hours, and exploring various applications and advanced scenarios.
Understanding Unit Rates
A unit rate is a ratio that compares a quantity to one unit of another quantity. It expresses the amount of one thing per single unit of another. Common examples include miles per hour (mph), price per pound, cost per item, and words per minute. The key is always having a denominator of '1'.
The provided example – 180 miles in 3 hours – asks us to find the unit rate of speed. In this context, we want to determine how many miles are traveled in one hour.
Calculating the Unit Rate: Miles Per Hour
To find the unit rate for 180 miles in 3 hours, we perform a simple division:
180 miles / 3 hours = 60 miles/hour
Therefore, the unit rate is 60 miles per hour. This means the average speed was 60 miles for every single hour of travel.
Step-by-Step Breakdown:
-
Identify the quantities: We have 180 miles (distance) and 3 hours (time).
-
Determine the desired unit rate: We want to find miles per hour (miles/hour).
-
Set up the ratio: Write the ratio as a fraction: 180 miles / 3 hours
-
Simplify the fraction: Divide the numerator (180 miles) by the denominator (3 hours).
-
State the unit rate: The result, 60 miles/hour, is the unit rate.
Real-World Applications of Unit Rates
Understanding unit rates is crucial for making informed decisions in many everyday situations:
1. Comparing Prices:
Imagine you're shopping for groceries. One store sells a 10-ounce bag of chips for $3.00, while another sells a 15-ounce bag for $4.20. To determine which is the better deal, you need to calculate the unit price (price per ounce):
- Store 1: $3.00 / 10 ounces = $0.30 per ounce
- Store 2: $4.20 / 15 ounces = $0.28 per ounce
Store 2 offers a lower unit price, making it the better value.
2. Calculating Speed and Distance:
Knowing unit rates is fundamental in understanding speed, distance, and time relationships. If you're driving at 55 mph and need to travel 330 miles, you can calculate the travel time:
330 miles / 55 mph = 6 hours
3. Determining Pay Rates:
If you earn $240 for 8 hours of work, your hourly wage (unit rate) is:
$240 / 8 hours = $30 per hour
4. Comparing Fuel Efficiency:
Fuel efficiency is often expressed in miles per gallon (mpg). Understanding unit rates helps you compare the fuel economy of different vehicles. A vehicle with higher mpg travels more miles on a gallon of fuel.
5. Productivity Measurement:
Unit rates are also utilized in measuring productivity. For example, words per minute (wpm) for typing speed, items produced per hour in a factory, or tasks completed per day.
Advanced Scenarios and Complex Unit Rates
The concept of unit rates extends beyond simple divisions. Let's explore some more complex situations:
1. Converting Units:
Sometimes, you need to convert units before calculating the unit rate. For example, if you travel 24 kilometers in 2 hours, and you want the unit rate in miles per hour, you'll need to convert kilometers to miles first. (Approximately 1 km = 0.621 miles)
24 km * 0.621 miles/km = 14.904 miles
Then calculate the unit rate:
14.904 miles / 2 hours = 7.452 miles/hour
2. Multiple Unit Rates:
In some cases, you may have multiple quantities to consider. For instance, imagine a worker earns $180 for a 6-hour workday, and uses 3 gallons of gas for his commute to and from work. To determine the hourly wage and the cost per hour of gas, you'd need to calculate two separate unit rates:
- Hourly wage: $180 / 6 hours = $30/hour
- Gas cost per hour: Let's assume gas costs $4 per gallon. Total gas cost = 3 gallons * $4/gallon = $12. Gas cost per hour = $12 / 6 hours = $2/hour
3. Rates with Compound Units:
Sometimes, you'll encounter rates with compound units, such as miles per gallon per hour. This might represent fuel efficiency considering both speed and distance. Such calculations might involve more complex mathematical operations beyond simple division.
Mastering Unit Rates: Tips and Tricks
-
Always identify the units: Clearly define the units involved in the problem to avoid errors.
-
Convert units if necessary: Ensure consistent units before calculating the unit rate.
-
Use labels: Write out the units with your numbers to keep track of the quantities. (e.g., 180 miles / 3 hours)
-
Check your answer: Ensure your answer is reasonable and makes sense within the context of the problem.
-
Practice Regularly: The best way to master unit rates is through consistent practice and solving a variety of problems.
Conclusion: The Power of Unit Rates
The ability to calculate and interpret unit rates is a versatile and essential skill in numerous aspects of life. From making informed consumer decisions to understanding speed and productivity, mastering unit rates empowers you to analyze data, make comparisons, and solve real-world problems effectively. By consistently practicing and applying these concepts, you'll gain a strong foundation in mathematical reasoning and problem-solving. This improved understanding will not only help you in academic settings but also provide invaluable tools for navigating everyday scenarios with increased confidence and efficiency. Remember to break down complex problems into smaller, manageable steps, focusing on clear identification of units and careful execution of calculations. With practice and attention to detail, you’ll master the art of finding unit rates and unlock their practical power.
Latest Posts
Latest Posts
-
How Many Days Has It Been Since September 2022
May 15, 2025
-
Is Uv Index 6 Good For Tanning
May 15, 2025
-
How Many More Hours Until 7 Pm Today
May 15, 2025
-
What Is 450 Ml In Cups
May 15, 2025
-
How Much Is 35 Square Meters
May 15, 2025
Related Post
Thank you for visiting our website which covers about Find The Unit Rate. 180 Miles In 3 Hours . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.