Find Z If 1 4/11 Of Z Is 45
Treneri
May 10, 2025 · 4 min read
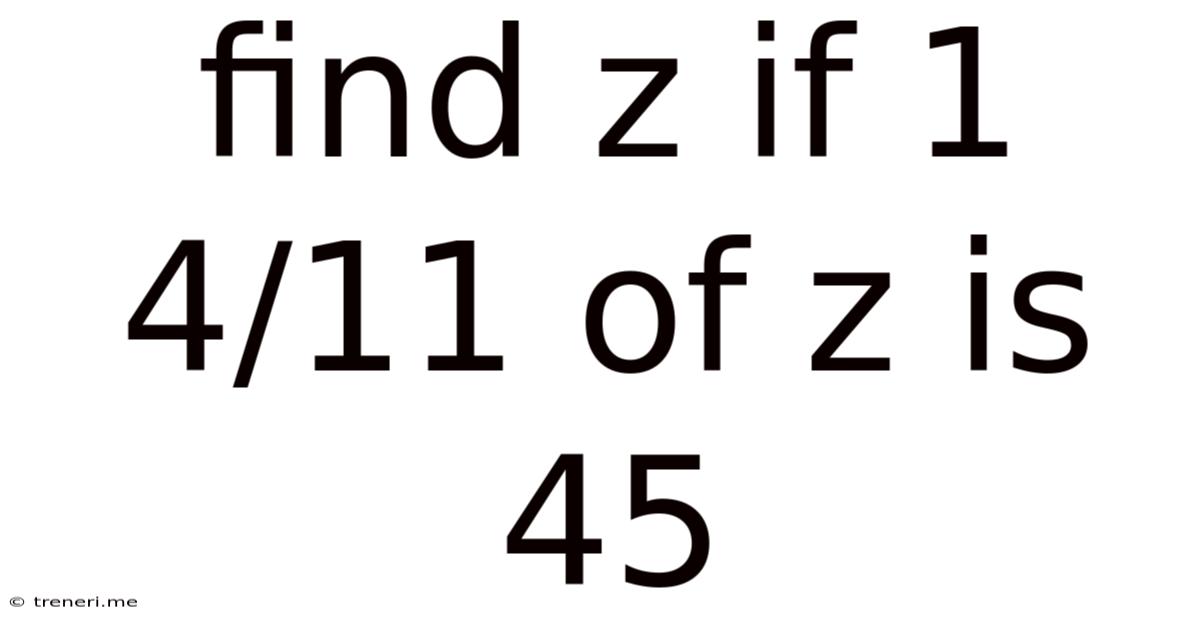
Table of Contents
Find Z if 1 4/11 of Z is 45: A Comprehensive Guide to Solving Mixed Number Equations
This article provides a comprehensive guide on how to solve the equation "1 4/11 of z is 45," explaining the process step-by-step, offering different approaches, and exploring the underlying mathematical concepts. We'll delve into the intricacies of working with mixed numbers, converting them into improper fractions, and ultimately, isolating the variable 'z' to find its value. We’ll also discuss how to check your answer for accuracy and explore similar problem types to solidify your understanding.
Understanding the Problem: Deconstructing "1 4/11 of z is 45"
The statement "1 4/11 of z is 45" can be translated into a mathematical equation. The phrase "of" in mathematics signifies multiplication. Therefore, the equation becomes:
(1 4/11) * z = 45
This equation involves a mixed number (1 4/11), a variable (z), and a constant (45). Our goal is to solve for the value of 'z'.
Method 1: Converting the Mixed Number to an Improper Fraction
The first and most common method involves converting the mixed number 1 4/11 into an improper fraction. This makes the equation easier to manipulate.
Step 1: Convert the mixed number to an improper fraction.
To convert a mixed number to an improper fraction, we multiply the whole number (1) by the denominator (11), add the numerator (4), and place the result over the original denominator:
1 * 11 + 4 = 15
Therefore, 1 4/11 becomes 15/11.
Step 2: Rewrite the equation.
Substitute the improper fraction into the original equation:
(15/11) * z = 45
Step 3: Solve for z.
To isolate 'z', we multiply both sides of the equation by the reciprocal of 15/11, which is 11/15:
(11/15) * (15/11) * z = 45 * (11/15)
This simplifies to:
z = 45 * (11/15)
Now, we can simplify the fraction and perform the multiplication:
z = (45/1) * (11/15) We can cancel out the common factor 15:
z = 3 * 11
z = 33
Therefore, the value of z is 33.
Method 2: Solving Directly with the Mixed Number (A More Advanced Approach)
While converting to an improper fraction is generally recommended, we can also solve this directly using the mixed number. This method demonstrates a slightly more advanced understanding of fraction manipulation.
Step 1: Distribute the mixed number.
We can rewrite the mixed number as a sum: 1 + 4/11. This allows us to distribute it to 'z':
(1 + 4/11) * z = 45
This becomes:
z + (4/11)z = 45
Step 2: Combine the 'z' terms.
We can factor out 'z':
z(1 + 4/11) = 45
Step 3: Simplify the expression in the parentheses.
Adding 1 and 4/11:
1 + 4/11 = (11/11) + (4/11) = 15/11
So the equation becomes:
(15/11)z = 45
Step 4: Solve for z.
This is the same equation we arrived at in Method 1. Multiplying both sides by 11/15, we again find:
z = 33
Verifying the Solution
It's crucial to verify our solution to ensure accuracy. We substitute z = 33 back into the original equation:
(1 4/11) * 33 = 45
Converting 1 4/11 to an improper fraction (15/11):
(15/11) * 33 = 45
Simplifying:
15 * 3 = 45
45 = 45
The equation holds true, confirming that our solution, z = 33, is correct.
Expanding the Understanding: Similar Problem Types
Understanding this problem allows you to tackle similar equations involving mixed numbers and variables. Here are some examples:
-
2 1/3 of x = 14: This equation follows the same structure. Convert 2 1/3 to an improper fraction (7/3), then solve for x using the same method described above.
-
3/5 of y + 2 = 8: This equation is slightly more complex, requiring you to isolate the term with 'y' before solving. Subtract 2 from both sides, then solve for y.
-
(a + 2/7) * 5 = 25: This involves a sum within the parentheses. First, divide both sides by 5, then solve for 'a'.
Practical Applications
Solving equations involving mixed numbers is essential in many real-world scenarios:
-
Baking and Cooking: Recipes often use mixed numbers for ingredient quantities. Scaling a recipe up or down requires solving similar equations.
-
Construction and Engineering: Calculations involving dimensions and materials frequently involve mixed numbers.
-
Finance: Calculating interest, discounts, and other financial computations often involve fractions and mixed numbers.
-
Data Analysis: Working with statistical data may involve mixed numbers that need to be manipulated and analyzed.
Mastering Mixed Number Equations: Practice and Further Exploration
The ability to confidently solve equations like "1 4/11 of z is 45" is a fundamental skill in mathematics. Consistent practice is key to mastering these techniques. Work through various problem types, ensuring you understand each step and the underlying concepts. Don't hesitate to explore online resources or seek additional help if needed. With consistent effort, you'll develop a strong foundation in solving equations that involve mixed numbers and fractions. This skill will serve you well in many academic and professional endeavors. Remember to always check your work for accuracy to ensure you’ve found the correct solution. The more you practice, the more confident and proficient you'll become in tackling these types of mathematical problems.
Latest Posts
Latest Posts
-
1 Cubic Foot Water In Gallons
May 10, 2025
-
Tabla De Aumento De Peso En El Embarazo
May 10, 2025
-
4186 6 Rounded To The Nearest Hundredth
May 10, 2025
-
Greatest Common Factor Of 30 And 75
May 10, 2025
-
What Is 645 Rounded To The Nearest Ten
May 10, 2025
Related Post
Thank you for visiting our website which covers about Find Z If 1 4/11 Of Z Is 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.