Formula For The Diameter Of A Cylinder
Treneri
Apr 06, 2025 · 5 min read
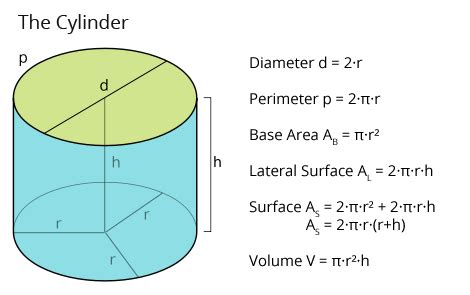
Table of Contents
The Ultimate Guide to Calculating the Diameter of a Cylinder
Determining the diameter of a cylinder is a fundamental concept in geometry and engineering, with applications spanning various fields. From calculating the volume of a storage tank to designing engine components, understanding how to find the diameter is crucial. This comprehensive guide delves deep into the formulas, explores different scenarios, and offers practical examples to solidify your understanding. We'll also touch upon related concepts and potential challenges you might encounter.
Understanding Cylindrical Geometry
Before diving into the formulas, let's establish a clear understanding of cylinder terminology. A cylinder is a three-dimensional solid composed of two parallel circular bases connected by a curved surface. Key components include:
- Diameter (d): The distance across the circle, passing through the center. This is the primary focus of our guide.
- Radius (r): Half the diameter. The distance from the center of the circular base to any point on the circumference. The relationship is:
r = d/2ord = 2r. - Height (h) or Length (l): The perpendicular distance between the two circular bases.
- Circumference (C): The distance around the circular base. Calculated as
C = πdorC = 2πr.
Formulas for Calculating Cylinder Diameter
The method used to calculate the diameter depends on what information is available. Here are the most common scenarios:
1. Using the Radius:
This is the most straightforward approach. If you know the radius (r), the diameter (d) is simply twice the radius:
Formula: d = 2r
Example: If the radius of a cylinder is 5 cm, its diameter is 2 * 5 cm = 10 cm.
2. Using the Circumference:
If the circumference (C) is known, you can use the following formula to determine the diameter:
Formula: d = C/π
This formula is derived directly from the circumference formula (C = πd). Remember to use the appropriate value of π (pi), typically 3.14159 or the value provided by your calculator.
Example: If the circumference of a cylinder is 31.4 cm, its diameter is 31.4 cm / π ≈ 10 cm.
3. Using the Volume and Height:
In cases where the volume (V) and height (h) of the cylinder are known, you can indirectly calculate the diameter. The formula for the volume of a cylinder is:
Formula (Volume): V = πr²h
To find the diameter, first solve for the radius:
Formula (Radius from Volume): r = √(V/(πh))
Then, double the radius to get the diameter:
Formula (Diameter from Volume): d = 2√(V/(πh))
Example: A cylinder has a volume of 157 cubic centimeters and a height of 5 centimeters. Therefore:
r = √(157 cm³ / (π * 5 cm)) ≈ 3.16 cm
d = 2 * 3.16 cm ≈ 6.32 cm
4. Using the Surface Area:
The surface area (A) of a cylinder is given by the formula:
Formula (Surface Area): A = 2πr² + 2πrh
While this formula doesn't directly give you the diameter, you can solve for the radius and then calculate the diameter. This approach is more complex and typically requires using quadratic equations. This will be expanded on in the more advanced section.
Practical Applications and Real-World Examples
The ability to calculate cylinder diameters finds widespread applications in various fields:
- Engineering: Designing pipes, gears, pistons, and other cylindrical components. Accurate diameter calculations are critical for proper fit and function.
- Manufacturing: Ensuring the consistency of manufactured goods. Quality control often involves measuring diameters to ensure adherence to specifications.
- Construction: Calculating the volume of cylindrical storage tanks, silos, or pipes for water or other materials. This directly impacts project planning and material costs.
- Packaging: Designing cylindrical containers for products. Optimizing the diameter minimizes material usage while maintaining product protection.
- Science: Analyzing cylindrical samples in experiments, calculations in fluid dynamics, and other scientific fields that involve three-dimensional objects.
Advanced Considerations and Challenges
While the basic formulas are relatively straightforward, certain situations might present more complex calculations:
-
Calculating Diameter from Surface Area: As mentioned earlier, using the surface area formula to derive the diameter requires solving a quadratic equation. This involves more mathematical steps and understanding of quadratic equation solving techniques.
-
Dealing with Incomplete Information: If you don't have sufficient information (e.g., only knowing the volume without the height), you won't be able to calculate the diameter directly. Additional measurements will be needed.
-
Measurement Errors: In real-world scenarios, measurements can be imprecise. The accuracy of your diameter calculation will be influenced by the accuracy of your initial measurements. Consider using precision measurement tools to minimize errors.
-
Non-Circular Bases: The formulas we've discussed assume perfectly circular bases. If the bases are slightly elliptical or irregular, more advanced techniques (perhaps involving calculus) might be necessary for accurate diameter determination.
Troubleshooting and Tips for Accurate Calculations:
- Use accurate measurements: Employ precise measuring instruments, such as calipers or micrometers, for better accuracy.
- Employ the appropriate formula: Select the formula that aligns with the information you possess.
- Use a consistent unit system: Stick to a single unit system (e.g., centimeters, inches) throughout your calculations.
- Double-check your calculations: It's crucial to verify your work to minimize errors. Use a calculator for complex calculations.
- Consider approximations: In many scenarios, using an approximation of π (3.14) is sufficient. However, for higher precision, use your calculator's value of π.
Conclusion
Understanding how to calculate the diameter of a cylinder is essential across many disciplines. By grasping the fundamental formulas and considering the potential complexities, you can effectively tackle a wide range of problems involving cylindrical objects. Remember to choose the correct formula based on the available information and pay close attention to accuracy in measurements and calculations. The information provided here serves as a solid foundation for tackling more advanced problems related to cylindrical geometry and its applications.
Latest Posts
Latest Posts
-
Convert Minced Garlic To Garlic Powder
Apr 07, 2025
-
How Many Days Are 8 Weeks
Apr 07, 2025
-
Consumer Surplus Calculator From Demand Function
Apr 07, 2025
-
What Is The Volume Of The Cone Below 84 11
Apr 07, 2025
-
How Many Grams Of Water Are In A Gallon
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Formula For The Diameter Of A Cylinder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.