Formula For The Height Of A Trapezoid
Treneri
Apr 04, 2025 · 5 min read
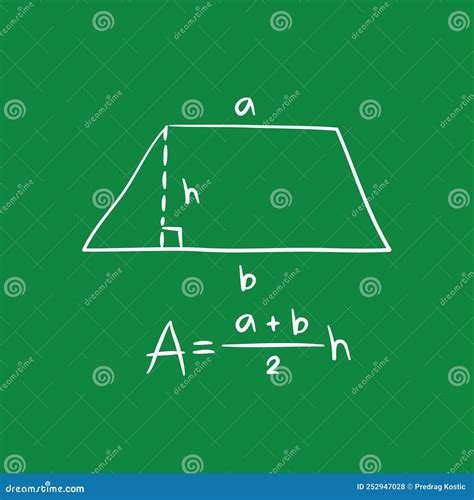
Table of Contents
The Comprehensive Guide to Calculating the Height of a Trapezoid
The trapezoid, a quadrilateral with at least one pair of parallel sides, presents a unique challenge in geometric calculations. While finding the area is a common task, determining the height of a trapezoid requires a deeper understanding of its properties and the application of various formulas. This comprehensive guide will delve into the different methods for calculating the height, catering to various scenarios and levels of mathematical expertise. We'll explore the core concepts, provide step-by-step examples, and address common pitfalls to ensure a thorough grasp of this crucial geometric concept.
Understanding the Trapezoid and its Components
Before diving into the formulas, let's establish a firm understanding of the trapezoid's key components:
- Bases (b1 and b2): These are the two parallel sides of the trapezoid. It's crucial to identify these correctly as they are fundamental to the height calculation.
- Legs (a and c): These are the two non-parallel sides. While not directly involved in the basic height formula, they play a role in more advanced scenarios.
- Height (h): This is the perpendicular distance between the two bases. It's the key element we aim to calculate.
Formula 1: Using Area and Base Lengths
The most straightforward method to determine the height of a trapezoid involves its area and the lengths of its bases. The formula is derived from the fundamental area formula for a trapezoid:
Area = (1/2) * (b1 + b2) * h
To solve for the height (h), we simply rearrange the formula:
h = (2 * Area) / (b1 + b2)
Example:
Let's say we have a trapezoid with an area of 30 square units, a base (b1) of 4 units, and another base (b2) of 8 units. Applying the formula:
h = (2 * 30) / (4 + 8) = 60 / 12 = 5 units
Therefore, the height of the trapezoid is 5 units.
Important Note: This method requires knowing the area of the trapezoid. If the area isn't provided, you'll need to employ alternative methods discussed later.
Formula 2: Using Trigonometry (Right-Angled Triangles)
When dealing with right-angled trapezoids or trapezoids where you know an angle and the length of one leg, trigonometry provides a powerful solution. This method involves constructing a right-angled triangle within the trapezoid and utilizing trigonometric functions such as sine, cosine, or tangent.
Example:
Imagine a right-angled trapezoid where one leg (a) is 6 units long, and the angle between that leg and the longer base (b2) is 30 degrees. The difference between the bases (b2 - b1) acts as the base of the right-angled triangle.
First, we determine the height using the sine function:
sin(30°) = h / a
h = a * sin(30°) = 6 * 0.5 = 3 units
Therefore, the height of the trapezoid is 3 units. Similar trigonometric approaches can be used with other angles and side lengths, adapting the specific trigonometric function according to the available information. Remember to always correctly identify the relevant triangle within the trapezoid.
Important Note: The success of this method depends on having sufficient information about angles and side lengths within the trapezoid. Incorrect angle or side identification will lead to an inaccurate height calculation.
Formula 3: Using Coordinate Geometry
If the trapezoid's vertices are defined by coordinates on a Cartesian plane, we can leverage the distance formula and the concept of slope to calculate the height.
Example:
Let's say the vertices of a trapezoid are A(1,1), B(5,1), C(4,4), and D(2,4). The bases are AB and CD, which are parallel to the x-axis. The height is the vertical distance between the bases. We simply subtract the y-coordinates of the vertices on the parallel sides:
Height = 4 - 1 = 3 units
Advanced Coordinate Geometry:
For trapezoids not aligned with the axes, the process is slightly more complex. We'd need to:
- Find the equation of the line representing one base.
- Find the perpendicular distance from a point on the opposite base to this line. This involves using the formula for the distance between a point and a line. This formula is more advanced and requires a stronger understanding of coordinate geometry.
Formula 4: Dividing into Rectangles and Triangles
For irregular trapezoids, especially those where other methods prove difficult, dividing the trapezoid into simpler shapes (rectangles and triangles) can be beneficial. This involves calculating the height of the constructed rectangle and potentially using Pythagorean theorem for the triangles. This method is particularly useful when dealing with trapezoids lacking symmetry or right angles.
Example:
Consider a trapezoid that can be divided into a rectangle and two right-angled triangles. If we know the base lengths and the lengths of the legs, we can use the Pythagorean theorem to find the height of the triangles and thus, the height of the rectangle, which is the same as the height of the trapezoid.
Pitfalls to Avoid
- Incorrect Base Identification: Always double-check that you've correctly identified the parallel bases before applying any formula.
- Unit Consistency: Ensure all measurements (area, base lengths, etc.) are in the same units to prevent inaccurate results.
- Angle Measurement: When using trigonometry, ensure angle measurements are in the correct units (degrees or radians).
- Rounding Errors: Avoid premature rounding during calculations. Round only the final answer to the desired level of precision.
- Assumptions: Don't make assumptions about the trapezoid's properties (e.g., assuming it's isosceles without proof).
Conclusion: Mastering Trapezoid Height Calculations
Calculating the height of a trapezoid is a fundamental skill in geometry with applications in various fields, including architecture, engineering, and computer graphics. While the basic formula involving area and base lengths is straightforward, understanding the alternative methods using trigonometry, coordinate geometry, and shape decomposition equips you to tackle diverse problems. By carefully selecting the appropriate method based on the available information and avoiding common pitfalls, you can confidently determine the height of any trapezoid and leverage this knowledge for more complex geometric calculations. Remember to practice regularly and apply these techniques to various problems to enhance your understanding and proficiency. This comprehensive guide provides a robust foundation for tackling a wide range of trapezoid height challenges.
Latest Posts
Latest Posts
-
How Many Reps Of 185 To Bench 225
Apr 04, 2025
-
How Many Fridays Between September 2022 And June 2024
Apr 04, 2025
-
If Your Born In 2004 How Old Are You
Apr 04, 2025
-
180 Days From July 2 2024
Apr 04, 2025
-
How Big Is 30 Sq Ft
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Formula For The Height Of A Trapezoid . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
