Gcf Of 16 20 And 24
Treneri
May 11, 2025 · 5 min read
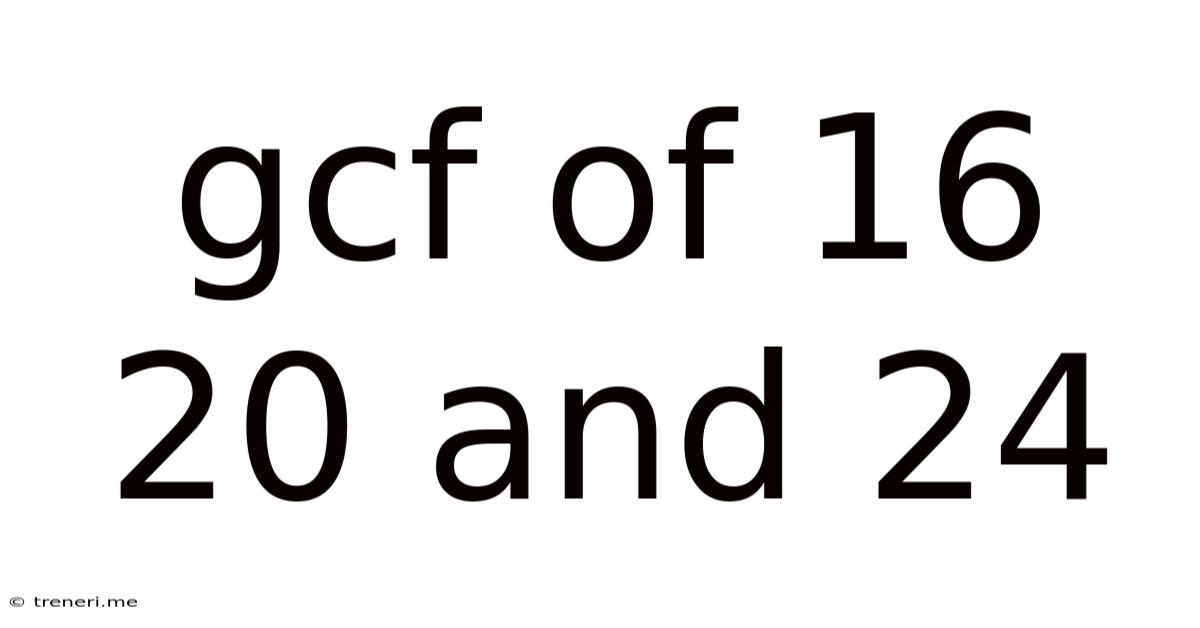
Table of Contents
Finding the Greatest Common Factor (GCF) of 16, 20, and 24: A Comprehensive Guide
Finding the greatest common factor (GCF) of a set of numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This comprehensive guide will delve into various methods for determining the GCF, focusing specifically on finding the GCF of 16, 20, and 24. We'll explore different approaches, explain the underlying principles, and provide practical examples to solidify your understanding.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers in a given set without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into all the numbers in your set. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Method 1: Prime Factorization
Prime factorization is a powerful method for finding the GCF of any set of numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Once you have the prime factorization of each number, you can identify the common prime factors and their lowest powers to find the GCF.
Let's apply this method to find the GCF of 16, 20, and 24:
1. Prime Factorization of 16:
16 = 2 x 8 = 2 x 2 x 4 = 2 x 2 x 2 x 2 = 2<sup>4</sup>
2. Prime Factorization of 20:
20 = 2 x 10 = 2 x 2 x 5 = 2<sup>2</sup> x 5
3. Prime Factorization of 24:
24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2<sup>3</sup> x 3
4. Identifying Common Prime Factors:
The only common prime factor among 16, 20, and 24 is 2.
5. Determining the Lowest Power:
The lowest power of 2 among the factorizations is 2<sup>2</sup> (from the factorization of 20).
6. Calculating the GCF:
Therefore, the GCF of 16, 20, and 24 is 2<sup>2</sup> = 4.
Method 2: Listing Factors
This method is suitable for smaller numbers. It involves listing all the factors of each number and then identifying the largest factor common to all.
1. Factors of 16: 1, 2, 4, 8, 16
2. Factors of 20: 1, 2, 4, 5, 10, 20
3. Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
4. Common Factors: The common factors of 16, 20, and 24 are 1, 2, and 4.
5. Greatest Common Factor: The largest of these common factors is 4.
Therefore, the GCF of 16, 20, and 24 is 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, and it can be extended to find the GCF of multiple numbers by applying it iteratively. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
To find the GCF of 16, 20, and 24 using the Euclidean algorithm, we can proceed as follows:
1. Find the GCF of 16 and 20:
- 20 = 16 x 1 + 4
- 16 = 4 x 4 + 0
The GCF of 16 and 20 is 4.
2. Find the GCF of 4 and 24:
- 24 = 4 x 6 + 0
The GCF of 4 and 24 is 4.
Therefore, the GCF of 16, 20, and 24 is 4.
Applications of the GCF
The GCF has numerous applications across various mathematical fields and real-world scenarios:
1. Simplifying Fractions:
The GCF is crucial for simplifying fractions to their lowest terms. For instance, to simplify the fraction 24/16, we find the GCF of 24 and 16, which is 8. Dividing both the numerator and denominator by 8 gives us the simplified fraction 3/2.
2. Solving Algebraic Equations:
The GCF is often used to factor algebraic expressions. Factoring expressions simplifies them and makes it easier to solve equations. For example, factoring the expression 16x + 20y involves finding the GCF of 16 and 20, which is 4. The factored expression is 4(4x + 5y).
3. Real-World Applications:
The GCF has practical applications in various real-world situations, such as:
-
Dividing objects into equal groups: Imagine you have 16 apples, 20 oranges, and 24 bananas. To divide these fruits into the largest possible equal groups without any leftovers, you'd use the GCF (which is 4), creating 4 groups each containing 4 apples, 5 oranges, and 6 bananas.
-
Tile arrangements: When arranging square tiles to cover a rectangular area, the GCF helps determine the largest possible tile size that can be used without needing to cut any tiles.
Conclusion: Mastering the GCF
Understanding and mastering the calculation of the greatest common factor is essential for success in various mathematical endeavors. This guide has presented three effective methods – prime factorization, listing factors, and the Euclidean algorithm – each providing a different approach to finding the GCF. By understanding these methods and their applications, you'll be well-equipped to tackle GCF problems with confidence and solve a wide array of related mathematical challenges. Remember to choose the method that best suits the numbers involved for efficiency and ease of calculation. The GCF, seemingly a simple concept, unlocks a wealth of possibilities within mathematics and beyond. From simplifying fractions to tackling complex algebraic problems, the GCF forms a cornerstone of mathematical understanding.
Latest Posts
Latest Posts
-
60 Days From May 14 2024
May 12, 2025
-
What Is 25 Percent Of 24
May 12, 2025
-
Odds Of Winning A Raffle Calculator
May 12, 2025
-
Is 5 Uv Index Good For Tanning
May 12, 2025
-
120 Days From May 3 2024
May 12, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 20 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.