Gcf Of 16 32 And 40
Treneri
May 14, 2025 · 5 min read
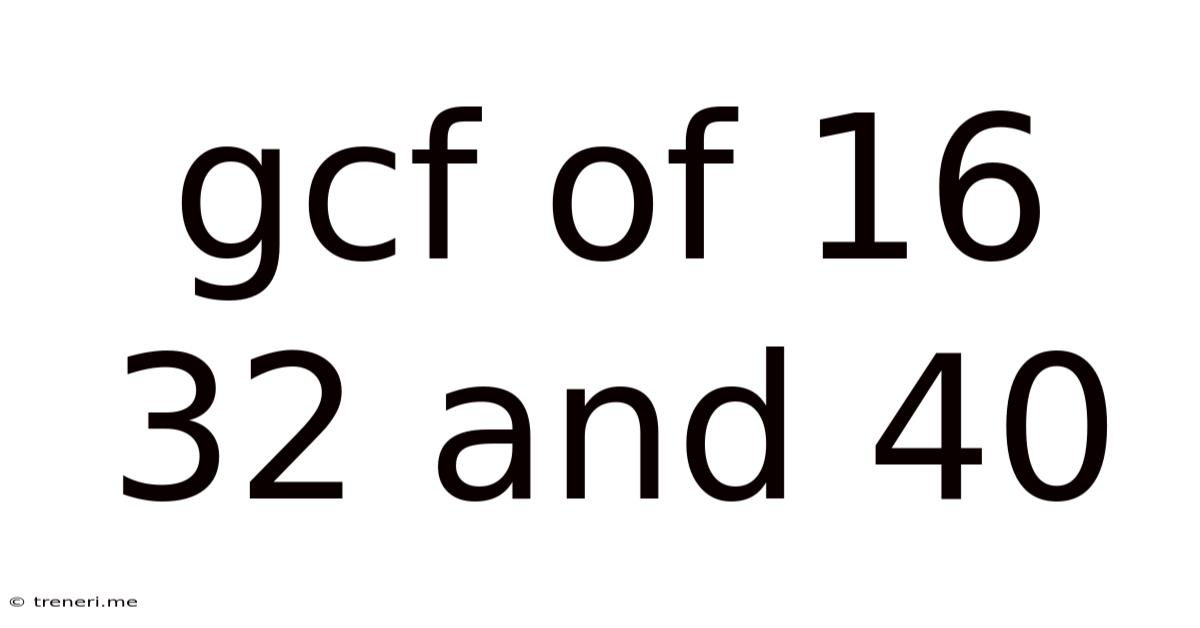
Table of Contents
Finding the Greatest Common Factor (GCF) of 16, 32, and 40: A Comprehensive Guide
Finding the greatest common factor (GCF) of numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This article delves deep into the process of determining the GCF of 16, 32, and 40, exploring multiple methods and explaining the underlying mathematical principles. We'll cover various techniques, including prime factorization, the Euclidean algorithm, and listing factors, to ensure a thorough understanding of this important mathematical operation. By the end, you'll not only know the GCF of these three numbers but also possess the skills to calculate the GCF of any set of numbers.
Understanding the Greatest Common Factor (GCF)
Before we embark on calculating the GCF of 16, 32, and 40, let's define the term precisely. The greatest common factor (GCF), also known as greatestcommon divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into all the numbers in the set evenly. This concept is crucial in various mathematical contexts, including simplification of fractions, factoring polynomials, and solving problems related to divisibility.
Method 1: Prime Factorization
This is arguably the most common and straightforward method for finding the GCF. It involves breaking down each number into its prime factors and then identifying the common prime factors raised to the lowest power.
Step 1: Prime Factorization of Each Number
- 16: 2 x 2 x 2 x 2 = 2<sup>4</sup>
- 32: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
- 40: 2 x 2 x 2 x 5 = 2<sup>3</sup> x 5
Step 2: Identifying Common Prime Factors
Observe that the only common prime factor among 16, 32, and 40 is 2.
Step 3: Determining the Lowest Power
The lowest power of 2 among the factorizations is 2<sup>3</sup> (from the factorization of 40).
Step 4: Calculating the GCF
Therefore, the GCF of 16, 32, and 40 is 2<sup>3</sup> = 8.
Method 2: Listing Factors
This method is simpler for smaller numbers but can become cumbersome for larger ones. It involves listing all the factors of each number and then identifying the largest factor common to all.
Step 1: Listing Factors of Each Number
- Factors of 16: 1, 2, 4, 8, 16
- Factors of 32: 1, 2, 4, 8, 16, 32
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Step 2: Identifying Common Factors
The common factors of 16, 32, and 40 are 1, 2, 4, and 8.
Step 3: Determining the Greatest Common Factor
The greatest among these common factors is 8. Therefore, the GCF of 16, 32, and 40 is 8.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF. To apply this to three numbers, we find the GCF of two numbers first, and then find the GCF of that result and the third number.
Step 1: Finding the GCF of 16 and 32
- 32 = 16 x 2 + 0 The remainder is 0, so the GCF of 16 and 32 is 16.
Step 2: Finding the GCF of 16 and 40
- 40 = 16 x 2 + 8
- 16 = 8 x 2 + 0 The remainder is 0, so the GCF of 16 and 40 is 8.
Step 3: The GCF of 16, 32, and 40
Since the GCF of 16 and 32 is 16, and the GCF of 16 and 40 is 8, the GCF of 16, 32, and 40 is 8.
Applications of GCF
The concept of the greatest common factor has wide-ranging applications across various mathematical domains:
-
Simplifying Fractions: The GCF allows us to simplify fractions to their lowest terms. For example, the fraction 32/40 can be simplified by dividing both the numerator and the denominator by their GCF, which is 8, resulting in the simplified fraction 4/5.
-
Solving Equations: GCF plays a role in solving algebraic equations, especially those involving factoring. Finding the common factors helps in simplifying and solving the equations.
-
Geometry Problems: GCF is used in geometry problems involving dividing shapes into smaller congruent shapes or determining the dimensions of rectangular areas.
-
Number Theory: GCF is fundamental to many concepts in number theory, including modular arithmetic and Diophantine equations.
-
Computer Science: The Euclidean algorithm, used for calculating GCF, is an essential algorithm in computer science due to its efficiency and applications in cryptography and other areas.
Beyond the Basics: Exploring Related Concepts
While we've focused on the GCF of 16, 32, and 40, understanding this concept opens doors to explore related mathematical ideas:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of all the given integers. It's closely related to the GCF, and the product of the GCF and LCM of two numbers is equal to the product of the two numbers.
-
Relative Primality: Two numbers are said to be relatively prime or coprime if their GCF is 1. This concept is important in number theory and various applications.
-
Modular Arithmetic: GCF plays a critical role in modular arithmetic, which deals with remainders after division.
Conclusion: Mastering the GCF
This comprehensive guide has demonstrated various methods for calculating the greatest common factor, specifically focusing on the numbers 16, 32, and 40. We've established that the GCF of these three numbers is 8, and we've explored different approaches – prime factorization, listing factors, and the Euclidean algorithm – to arrive at this conclusion. Understanding these methods not only allows you to solve specific GCF problems but also equips you with a deeper grasp of fundamental mathematical concepts that underpin many advanced topics. The applications of GCF extend far beyond simple calculations, highlighting its importance across diverse mathematical areas and real-world scenarios. Remember to practice these methods to solidify your understanding and master the calculation of the GCF for any set of numbers.
Latest Posts
Latest Posts
-
65 Out Of 80 As A Grade
May 14, 2025
-
How Many Days Has It Been Since September 5th
May 14, 2025
-
Cuanto Son 18 Libras En Kilos
May 14, 2025
-
How Much Sand For 4x4 Sandbox Calculator
May 14, 2025
-
Find The Surface Area Of The Figure Below
May 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 32 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.