How Do You Find Cubic Inches Of A Cylinder
Treneri
Apr 05, 2025 · 5 min read
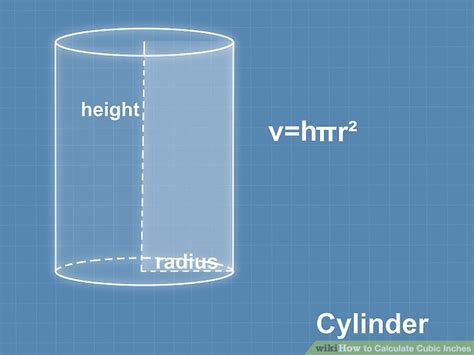
Table of Contents
How to Find the Cubic Inches of a Cylinder: A Comprehensive Guide
Calculating the volume of a cylinder, often expressed in cubic inches, is a fundamental concept in geometry and has widespread applications in various fields, from engineering and manufacturing to construction and everyday problem-solving. This comprehensive guide will walk you through the process, explaining the formula, providing step-by-step examples, addressing common mistakes, and exploring practical applications.
Understanding the Formula: The Heart of the Calculation
The volume of a cylinder is calculated using a straightforward formula:
Volume (V) = πr²h
Where:
- V represents the volume of the cylinder. This will be expressed in cubic units, such as cubic inches (in³), cubic centimeters (cm³), or cubic feet (ft³), depending on the units used for the radius and height.
- π (pi) is a mathematical constant, approximately equal to 3.14159. For most calculations, using 3.14 is sufficiently accurate, but for higher precision, you can use your calculator's π button.
- r represents the radius of the cylinder's circular base. The radius is half the diameter. Ensure that the radius and height are in the same units for consistent results.
- h represents the height of the cylinder. This is the perpendicular distance between the two circular bases. Again, maintain consistency with units.
Breaking Down the Formula: Why it Works
The formula itself combines two fundamental geometric concepts:
- πr²: This part calculates the area of the cylinder's circular base. Think of it as finding the area of a single circle.
- h: Multiplying the base area by the height essentially stacks multiple copies of that circular base on top of each other, filling up the three-dimensional space that defines the cylinder's volume.
Step-by-Step Calculation with Examples
Let's solidify our understanding with some practical examples. We will focus on finding the volume in cubic inches (in³).
Example 1: Simple Calculation
Let's say we have a cylinder with a radius (r) of 3 inches and a height (h) of 10 inches. Following the formula:
-
Calculate the area of the base: πr² = 3.14 * (3 in)² = 3.14 * 9 in² = 28.26 in²
-
Calculate the volume: V = πr²h = 28.26 in² * 10 in = 282.6 in³
Therefore, the volume of this cylinder is 282.6 cubic inches.
Example 2: Using the Diameter
Sometimes, you are given the diameter (d) instead of the radius. Remember, the radius is half the diameter (r = d/2).
Let's say a cylinder has a diameter of 6 inches and a height of 5 inches.
-
Calculate the radius: r = d/2 = 6 in / 2 = 3 in
-
Calculate the area of the base: πr² = 3.14 * (3 in)² = 28.26 in²
-
Calculate the volume: V = πr²h = 28.26 in² * 5 in = 141.3 in³
In this case, the volume of the cylinder is 141.3 cubic inches.
Example 3: Real-World Application: A Can of Soup
Imagine a can of soup with a diameter of 3 inches and a height of 4 inches. Let's find its volume.
-
Calculate the radius: r = d/2 = 3 in / 2 = 1.5 in
-
Calculate the area of the base: πr² = 3.14 * (1.5 in)² = 7.065 in²
-
Calculate the volume: V = πr²h = 7.065 in² * 4 in = 28.26 in³
The soup can's volume is approximately 28.26 cubic inches.
Avoiding Common Mistakes: Pitfalls to Watch Out For
Several common mistakes can lead to inaccurate volume calculations:
-
Unit Inconsistency: Ensure your radius and height are in the same units (both inches, both centimeters, etc.). Mixing units will result in an incorrect volume.
-
Incorrect Radius Calculation: Remember that the radius is half the diameter. Using the diameter directly in the formula will significantly inflate the calculated volume.
-
Rounding Errors: While using 3.14 for π is acceptable for many applications, be aware that rounding off intermediate results can accumulate errors. For higher precision, use more decimal places for π or use your calculator's π function directly.
-
Incorrect Formula: Double-check that you are using the correct formula, πr²h, and not confusing it with the formulas for other shapes like spheres or cones.
Advanced Concepts and Applications
While the basic formula is sufficient for most situations, understanding some advanced concepts can be beneficial:
Calculating Volume with Different Units
The formula remains the same regardless of the units used. Just ensure consistency:
-
Cubic Centimeters (cm³): If the radius and height are in centimeters, the resulting volume will be in cubic centimeters.
-
Cubic Feet (ft³): If the radius and height are in feet, the resulting volume will be in cubic feet.
You can easily convert between cubic units using conversion factors. For example, there are 1728 cubic inches in a cubic foot (12 inches/foot * 12 inches/foot * 12 inches/foot = 1728).
Cylinders with Irregular Heights or Bases
While the standard formula assumes a perfectly straight cylinder with uniform circular bases, you might encounter cylinders with slight irregularities. In such cases, you might need to break the cylinder into smaller sections with more regular shapes or use more advanced mathematical techniques like integration to calculate the volume accurately.
Applications in Engineering and Design
Understanding cylinder volume calculations is crucial in various engineering disciplines:
-
Fluid Mechanics: Calculating the volume of cylindrical tanks or pipes is essential for determining fluid capacity and flow rates.
-
Mechanical Engineering: Designing pistons, cylinders, and other components requires accurate volume calculations to optimize performance and efficiency.
-
Civil Engineering: Calculating the volume of cylindrical columns or support structures is critical for structural design and material estimation.
Conclusion: Mastering Cylinder Volume Calculations
Calculating the cubic inches (or other units) of a cylinder is a fundamental skill with practical applications across numerous fields. By understanding the formula, following the steps carefully, and avoiding common errors, you can accurately determine the volume of any cylindrical object. This ability empowers you to solve real-world problems, design effectively, and contribute to various technical and practical endeavors. Remember that consistent units are key, and understanding the principles behind the formula enhances your understanding of three-dimensional geometry and its applications.
Latest Posts
Latest Posts
-
Cuanto Son 50 Libras En Kilos
Apr 06, 2025
-
27 Days Is How Many Weeks
Apr 06, 2025
-
How Many Minutes Until 3 00 Pm Today
Apr 06, 2025
-
Round 15 To The Nearest Ten
Apr 06, 2025
-
Common Multiple Of 3 4 5
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find Cubic Inches Of A Cylinder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
