How Many Sig Figs In 0.010
Treneri
May 13, 2025 · 5 min read
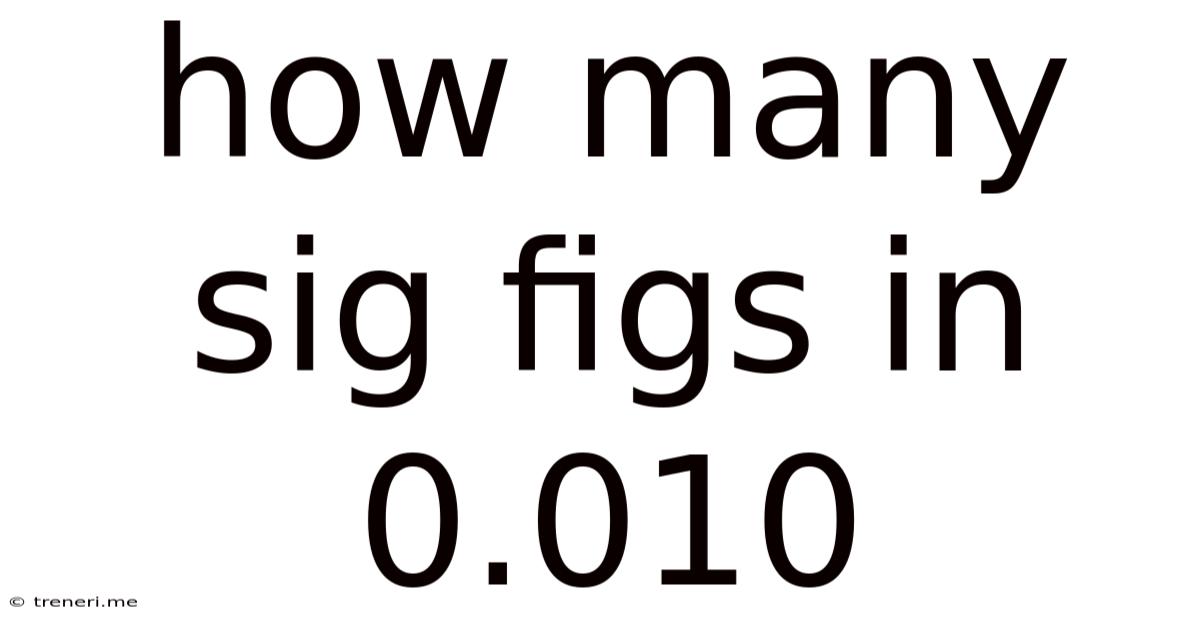
Table of Contents
How Many Significant Figures in 0.010? A Deep Dive into Significant Figures
Determining the number of significant figures (sig figs) in a number is crucial for accurate scientific calculations and data representation. Understanding significant figures ensures that the precision of measurements and calculations is correctly conveyed. This article will thoroughly explore the concept of significant figures, focusing specifically on the number 0.010 and providing a comprehensive guide to understanding and applying this essential concept in science and engineering.
Understanding Significant Figures
Significant figures represent the digits in a number that carry meaning contributing to its precision. They indicate the reliability and accuracy of a measurement or calculation. Zeroes play a particularly important role, sometimes contributing to significance, and sometimes not. Let's break down the rules:
Rules for Determining Significant Figures
-
Non-zero digits are always significant. For instance, in the number 123, all three digits are significant.
-
Zeroes between non-zero digits are always significant. In the number 102, the zero is significant.
-
Leading zeroes (zeroes to the left of the first non-zero digit) are never significant. These zeroes only serve to place the decimal point. For example, in 0.005, only the 5 is significant.
-
Trailing zeroes (zeroes to the right of the last non-zero digit) are significant only if the number contains a decimal point. This is a key rule. The number 100 has only one significant figure, while 100. has three, and 100.0 has four.
-
Trailing zeros in a number without a decimal point are ambiguous. For clarity, scientific notation is preferred.
Analyzing 0.010: How Many Significant Figures?
Now, let's apply these rules to the number 0.010.
-
Leading zeroes: The two zeroes to the left of the '1' are leading zeroes. According to rule 3, they are not significant.
-
The '1': The '1' is a non-zero digit, and according to rule 1, it is significant.
-
Trailing zero: The zero to the right of the '1' is a trailing zero. Because the number contains a decimal point (rule 4), this trailing zero is significant.
Therefore, the number 0.010 has two significant figures.
The Importance of Significant Figures in Calculations
Using the correct number of significant figures is vital in calculations to avoid propagating errors. The result of a calculation cannot be more precise than the least precise measurement used in the calculation. This principle guides the rules for rounding in calculations involving significant figures:
Rules for Rounding in Calculations
-
Addition and Subtraction: The result should have the same number of decimal places as the measurement with the fewest decimal places.
-
Multiplication and Division: The result should have the same number of significant figures as the measurement with the fewest significant figures.
Let's illustrate with examples:
Example 1 (Addition):
12.34 + 5.6 = 17.94
The result should be rounded to one decimal place (because 5.6 only has one decimal place), giving us 18.0.
Example 2 (Multiplication):
12.34 x 5.6 = 69.104
The result should be rounded to two significant figures (because 5.6 has only two significant figures), giving us 69.
Avoiding Ambiguity: The Power of Scientific Notation
Scientific notation is a powerful tool for removing ambiguity related to significant figures, particularly when dealing with trailing zeros. It expresses a number in the form of a coefficient multiplied by a power of 10.
For example, the number 0.010 can be written in scientific notation as 1.0 x 10⁻². This clearly shows that there are two significant figures. Similarly, 100 can be written as 1.0 x 10², indicating two significant figures, and 1.00 x 10², indicating three significant figures.
Practical Applications and Significance
The proper use of significant figures is not just an academic exercise; it's critical across numerous scientific and engineering fields. Accurate representation of measurements and calculated results directly impacts the reliability of:
- Engineering designs: Incorrect significant figures could lead to structural weaknesses or malfunctions in engineering projects.
- Medical dosages: Precise calculations are essential for accurate medication dosages, where errors can have severe consequences.
- Scientific research: Maintaining precision in data reporting and calculations is fundamental to the integrity and validity of scientific research findings.
- Environmental monitoring: Accurate measurements are crucial for understanding and addressing environmental challenges.
Common Mistakes to Avoid
Several common mistakes can lead to errors in determining and using significant figures. It's essential to be aware of these to ensure accuracy:
- Misinterpreting leading and trailing zeroes: Remember that leading zeroes are never significant, while trailing zeroes are significant only if a decimal point is present.
- Inconsistent rounding: Applying inconsistent rounding rules can introduce errors in calculations. Always follow the established rules for addition/subtraction and multiplication/division.
- Ignoring significant figures in calculations: Failing to consider significant figures during calculations can result in reporting results with an unwarranted level of precision.
Conclusion: Mastering Significant Figures for Precision
Understanding and correctly applying the rules of significant figures is paramount for accuracy and precision in any quantitative field. The number 0.010, with its leading and trailing zeroes, serves as a perfect example of the nuances involved in determining significance. By mastering these rules and utilizing tools like scientific notation, you can ensure your calculations and data representation reflect the true precision of your measurements, avoiding errors and maintaining the integrity of your work. Remember that accurate calculations are not just about getting the right answer; they're about correctly representing the precision of that answer, ensuring reliability and trust in your results. Continuous practice and a thorough understanding of the rules are key to achieving mastery in this crucial aspect of scientific and technical work.
Latest Posts
Latest Posts
-
184 Rounded To The Nearest Hundred
May 13, 2025
-
Calorie Counter For Breastfeeding Moms App
May 13, 2025
-
Cuantos Dias Han Pasado Desde Que Llegue A Usa
May 13, 2025
-
591 Rounded To The Nearest Ten
May 13, 2025
-
11 Oz Equals How Many Cups
May 13, 2025
Related Post
Thank you for visiting our website which covers about How Many Sig Figs In 0.010 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.