How Many Tenths Are In 2.8
Treneri
May 10, 2025 · 5 min read
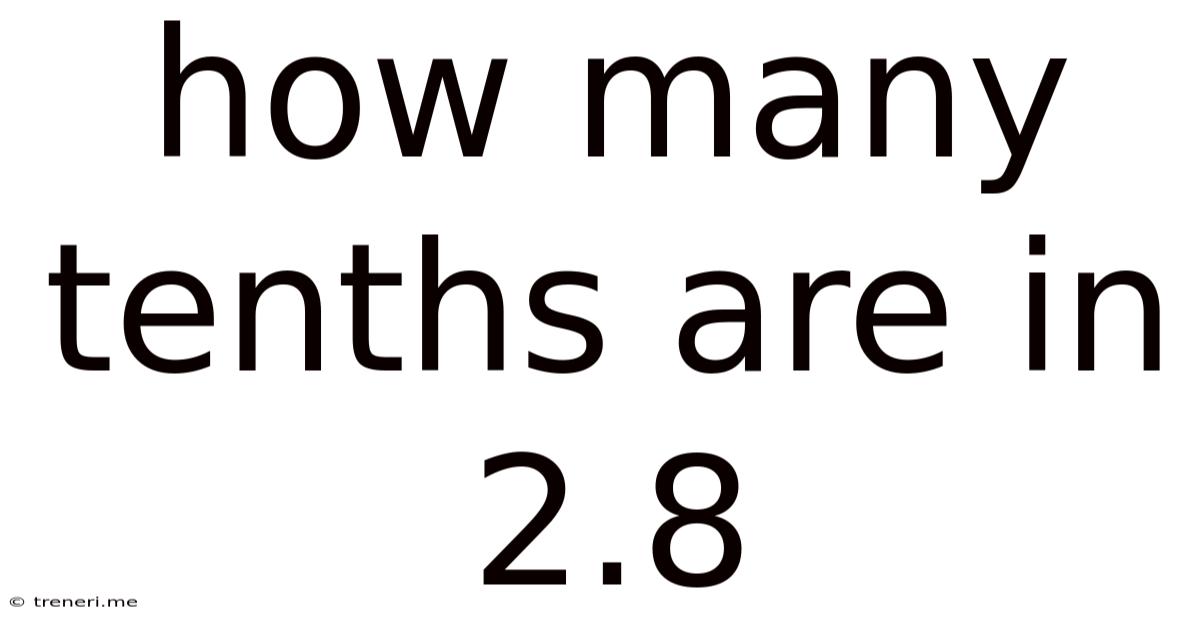
Table of Contents
How Many Tenths Are in 2.8? A Deep Dive into Decimal Understanding
Understanding decimals is fundamental to mathematics and numerous real-world applications. This seemingly simple question – "How many tenths are in 2.8?" – provides an excellent opportunity to explore the intricacies of decimal representation and its practical implications. We'll move beyond simply stating the answer and delve into the conceptual understanding necessary for mastering decimal operations.
Understanding Decimal Places and Place Value
Before tackling the specific problem, let's solidify our understanding of decimal places and place value. The decimal point separates the whole number portion from the fractional portion of a number. To the right of the decimal point, we have tenths, hundredths, thousandths, and so on. Each place value represents a power of ten.
- Ones: The place immediately to the left of the decimal point.
- Tenths: The first place to the right of the decimal point (1/10).
- Hundredths: The second place to the right of the decimal point (1/100).
- Thousandths: The third place to the right of the decimal point (1/1000).
And so on. Each place value is ten times smaller than the place value to its left. This systematic arrangement allows for precise representation of numbers smaller than one.
Breaking Down 2.8
The number 2.8 consists of two parts: a whole number part (2) and a decimal part (0.8). Let's focus on the decimal part, 0.8. The digit 8 is in the tenths place. This means it represents 8 tenths, or 8/10. Therefore, the number 2.8 can be written as:
- 2 + 0.8 (whole number + decimal fraction)
- 2 + 8/10 (whole number + fraction)
This clearly shows that there are 8 tenths in the decimal part of 2.8.
Visualizing Tenths
Visual aids can significantly improve understanding. Imagine a rectangle divided into ten equal parts. If you shade eight of these parts, you've shaded 8/10 or 0.8 of the rectangle. This visual representation reinforces the concept of tenths as parts of a whole. You can apply this visualization to any fraction represented in decimal form.
Connecting Fractions and Decimals
The ability to convert between fractions and decimals is critical for mastering decimal operations. The number 2.8 is equivalent to the mixed number 2 8/10. To convert a fraction to a decimal, divide the numerator by the denominator:
8 ÷ 10 = 0.8
This demonstrates the direct relationship between the fraction 8/10 and the decimal 0.8. Conversely, to convert a decimal to a fraction, you write the decimal part as the numerator and the appropriate power of 10 as the denominator. For example, 0.8 can be written as 8/10 which can be simplified to 4/5.
Expanding the Concept: Tenths in Larger Numbers
The question "How many tenths are in 2.8?" can be extended to explore the concept of tenths within larger numbers. Let's consider a number like 15.3. How many tenths are in this number?
First, we convert the whole number part to tenths. Since there are 10 tenths in each whole number, 15 whole numbers contain 15 * 10 = 150 tenths. Adding the 3 tenths from the decimal part, we have a total of 150 + 3 = 153 tenths in 15.3.
This exercise highlights the importance of understanding place value and the relationship between whole numbers and decimal fractions.
Real-World Applications of Decimal Understanding
Understanding decimals is not just an academic exercise; it's crucial in numerous real-world situations:
- Finance: Calculating monetary values, interest rates, taxes, and discounts all rely heavily on decimal calculations.
- Measurement: Expressing measurements of length, weight, volume, and temperature often involves decimals. For example, 2.8 meters or 2.8 kilograms.
- Science: Scientific data and measurements are commonly expressed using decimals, especially in fields like chemistry and physics.
- Engineering: Precision engineering requires accurate decimal calculations for design, manufacturing, and quality control.
- Data Analysis: Decimal representation is fundamental in statistical analysis, data visualization, and scientific research.
Advanced Concepts: Working with Different Decimal Places
While the initial question focused on tenths, understanding how to handle other decimal places is essential for comprehensive decimal mastery.
Let's say we want to find how many hundredths are in 2.8. Since there are 10 hundredths in one tenth, 2.8 (which has 8 tenths) contains 8 * 10 = 80 hundredths.
Similarly, to find the number of thousandths in 2.8, we multiply the number of hundredths by 10: 80 * 10 = 800 thousandths. This illustrates the consistent relationship between different decimal places.
Mastering Decimal Operations: Addition, Subtraction, Multiplication, and Division
Once you have a firm grasp of place value and decimal representation, you can confidently perform various arithmetic operations with decimals:
- Addition and Subtraction: Align the decimal points and perform the operations as you would with whole numbers.
- Multiplication: Multiply the numbers as you would with whole numbers, then count the total number of decimal places in the original numbers and place the decimal point in the product accordingly.
- Division: If the divisor is a decimal, multiply both the divisor and the dividend by a power of 10 to make the divisor a whole number. Then perform the division as you would with whole numbers.
Conclusion: The Importance of a Strong Decimal Foundation
The question "How many tenths are in 2.8?" serves as a springboard for a much deeper exploration of decimals. Understanding decimal place value, converting between fractions and decimals, performing arithmetic operations with decimals, and applying this knowledge to real-world situations are all crucial aspects of mathematical literacy. A strong foundation in decimals is essential for success in higher-level mathematics and numerous other fields. By mastering these concepts, you equip yourself with valuable tools for navigating a wide range of quantitative challenges. So, remember, there are 8 tenths in 2.8, but the real value lies in the understanding of the underlying principles.
Latest Posts
Latest Posts
-
Cuantos Ml Hay En Una Cucharada
May 10, 2025
-
If Your Born In 1971 How Old Are You
May 10, 2025
-
Cuantos Dias Faltan Para El 24 De Junio
May 10, 2025
-
How To Find Velocity With Acceleration And Distance
May 10, 2025
-
Greatest Common Factor Of 27 And 63
May 10, 2025
Related Post
Thank you for visiting our website which covers about How Many Tenths Are In 2.8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.