How To Find A Central Angle
Treneri
Apr 05, 2025 · 5 min read
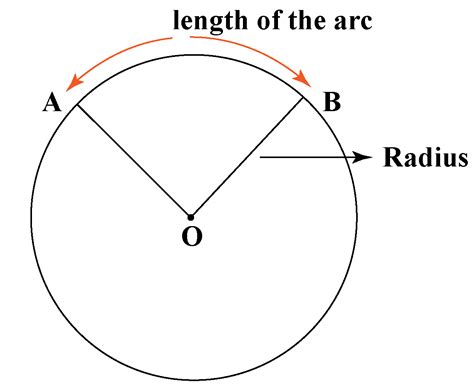
Table of Contents
How to Find a Central Angle: A Comprehensive Guide
Finding the measure of a central angle is a fundamental concept in geometry with applications in various fields, from architecture and engineering to computer graphics and cartography. This comprehensive guide will explore different methods for determining the central angle, covering various scenarios and providing practical examples to solidify your understanding.
Understanding Central Angles
Before diving into the methods, let's establish a clear understanding of what a central angle is. A central angle is an angle whose vertex (the point where two lines meet) is located at the center of a circle, and whose sides are radii (lines connecting the center to points on the circle) of that circle. The measure of a central angle is directly related to the length of the arc it subtends (cuts off) on the circle's circumference.
This relationship forms the basis for many calculations involving central angles.
Key Terms and Concepts
- Circle: A round plane figure whose boundary (the circumference) consists of points equidistant from a fixed center.
- Radius (r): The distance from the center of the circle to any point on the circumference.
- Diameter (d): A straight line passing from side to side through the center of a circle. It's twice the length of the radius (d = 2r).
- Circumference (C): The distance around the circle. Calculated using the formula C = 2πr, where π (pi) is approximately 3.14159.
- Arc: A portion of the circumference of a circle.
- Chord: A straight line segment whose endpoints both lie on the circumference of a circle.
- Sector: The region bounded by two radii and the arc they intercept.
Methods for Finding Central Angles
The method for finding a central angle depends on the information provided. Here are some common scenarios and their respective solutions:
1. Using the Arc Length and Radius
This is the most direct method, particularly useful when dealing with real-world applications where arc length might be measured directly. The formula connecting the central angle (θ), arc length (s), and radius (r) is:
θ = s / r (where θ is measured in radians)
To convert radians to degrees, use the conversion factor: 180° / π radians
Example:
An arc has a length of 10 cm and is part of a circle with a radius of 5 cm. Find the central angle in both radians and degrees.
- Radians: θ = 10 cm / 5 cm = 2 radians
- Degrees: θ = 2 radians * (180° / π radians) ≈ 114.59°
2. Using the Area of the Sector and Radius
If the area of the sector formed by the central angle is known, we can use the following formula:
Area of Sector = (θ/2) * r² (where θ is in radians)
Solving for θ:
θ = 2 * (Area of Sector) / r² (in radians)
Remember to convert radians to degrees as needed.
Example:
A sector of a circle with a radius of 8 cm has an area of 32 cm². Find the central angle.
- Radians: θ = 2 * (32 cm²) / (8 cm)² = 1 radian
- Degrees: θ = 1 radian * (180° / π radians) ≈ 57.3°
3. Using the Fraction of the Circle's Circumference
If the arc subtended by the central angle represents a known fraction of the circle's circumference, we can easily calculate the angle.
The central angle is directly proportional to the fraction of the circumference the arc represents. A full circle has a central angle of 360°. Therefore:
θ = (Arc Length / Circumference) * 360°
Example:
An arc represents one-quarter of a circle's circumference. Find the central angle.
- θ = (1/4) * 360° = 90°
4. Using Inscribed Angles
An inscribed angle is an angle whose vertex lies on the circle and whose sides are chords of the circle. The measure of an inscribed angle is half the measure of the central angle that subtends the same arc.
Therefore, if you know the measure of an inscribed angle subtending the same arc as the central angle:
θ (central angle) = 2 * θ (inscribed angle)
5. Using Trigonometric Functions (in Triangles)
If the central angle forms an isosceles triangle with two radii and a chord, trigonometric functions can be employed. Knowing the lengths of the radii and the chord, you can use the cosine rule or sine rule to determine the central angle.
For an isosceles triangle formed by two radii (r) and a chord (c):
c² = 2r² - 2r²cos(θ)
Solving for θ:
θ = cos⁻¹[(2r² - c²) / 2r²]
Example:
Two radii of a circle each measure 6cm, and the chord connecting their endpoints measures 8cm. Find the central angle.
- θ = cos⁻¹[(26² - 8²) / (26²)] ≈ 1.047 radians ≈ 60°
Practical Applications of Finding Central Angles
The ability to calculate central angles is crucial across many disciplines:
- Engineering: Designing gears, cams, and other rotating machinery. Understanding the angles of rotation is vital for precise mechanical operation.
- Architecture: Creating circular or arched structures, ensuring accurate dimensions and proportions.
- Cartography: Representing geographical areas on maps using projections that involve circular segments.
- Computer Graphics: Generating smooth curves and arcs in animations and computer-aided design (CAD) software.
- Physics: Calculating angular displacement and velocity in rotational motion.
- Astronomy: Determining the angular separation of celestial bodies.
Troubleshooting and Common Mistakes
- Unit Consistency: Ensure consistent units (e.g., centimeters for radius and arc length) throughout your calculations.
- Radian vs. Degrees: Remember to convert between radians and degrees as necessary using the conversion factor (180°/π radians).
- Correct Formula Selection: Choose the appropriate formula based on the given information.
- Calculator Settings: Ensure your calculator is set to the correct angle mode (degrees or radians).
Conclusion
Finding a central angle is a fundamental geometrical skill with broad applications. By mastering the various methods outlined in this guide, you'll be well-equipped to tackle a wide range of problems involving circles, arcs, and sectors. Remember to always carefully consider the information provided and select the appropriate formula for accurate results. Practice will solidify your understanding and improve your ability to solve central angle problems efficiently and confidently. With consistent practice and a clear understanding of the underlying principles, you'll become proficient in finding central angles and applying this knowledge to various real-world scenarios. Remember to always double-check your calculations and consider using different methods to verify your results for increased accuracy and confidence.
Latest Posts
Latest Posts
-
How Many Hours Are In 21 Days
Apr 05, 2025
-
9 Cups Is How Many Quarts
Apr 05, 2025
-
Dry Bulb Wet Bulb Temperature Relative Humidity Calculator
Apr 05, 2025
-
Find The Lateral Area Of The Cone
Apr 05, 2025
-
70 Grams Is How Many Ounces
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about How To Find A Central Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
