How To Find The Area Of A Decagon
Treneri
Apr 07, 2025 · 5 min read
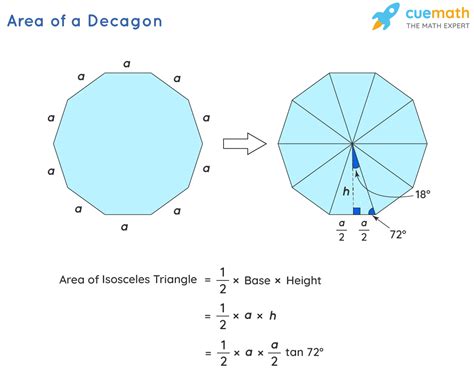
Table of Contents
How to Find the Area of a Decagon: A Comprehensive Guide
A decagon, a polygon with ten sides and ten angles, can seem daunting when it comes to calculating its area. However, with the right understanding of its geometric properties and a few formulas, finding the area of a decagon becomes a manageable task. This comprehensive guide breaks down various methods, catering to different levels of mathematical understanding, ensuring you'll master this geometric challenge.
Understanding Decagons: Regular vs. Irregular
Before diving into the area calculations, it's crucial to differentiate between regular and irregular decagons:
-
Regular Decagon: A regular decagon has all sides of equal length and all interior angles of equal measure (each angle measuring 144°). This symmetry simplifies area calculations significantly.
-
Irregular Decagon: An irregular decagon has sides and angles of varying lengths and measures. Calculating its area requires a more complex approach.
Methods for Calculating the Area of a Regular Decagon
For regular decagons, we can utilize several efficient methods:
Method 1: Using the Apothem and Perimeter
This is arguably the most straightforward method for calculating the area of a regular decagon. The formula is:
Area = (1/2) * apothem * perimeter
Where:
- Apothem: The distance from the center of the decagon to the midpoint of any side. Think of it as the radius of the inscribed circle.
- Perimeter: The total length of all ten sides. Since it's a regular decagon, this is simply 10 times the length of one side.
Example:
Let's say a regular decagon has a side length of 5 cm and an apothem of 7.69 cm.
- Perimeter: 10 sides * 5 cm/side = 50 cm
- Area: (1/2) * 7.69 cm * 50 cm = 192.25 cm²
This method elegantly connects the central properties of the decagon (apothem) to its overall dimensions (perimeter).
Method 2: Using the Side Length
If you only know the side length (s) of a regular decagon, you can use this formula derived from the apothem and perimeter method:
Area = (5/2) * s² * cot(π/10)
Where:
- s: The length of one side of the decagon.
- cot(π/10): The cotangent of π/10 radians (or 18°), a constant value approximately equal to 2.9069
Example:
With a side length (s) of 5 cm:
Area = (5/2) * 5² * cot(π/10) ≈ (5/2) * 25 * 2.9069 ≈ 181.68 cm² (Slight discrepancy due to rounding in cot(π/10)).
Method 3: Dividing into Triangles
A regular decagon can be divided into ten congruent isosceles triangles, each with a vertex at the center of the decagon. The area of each triangle can be calculated, then multiplied by ten to find the total area.
The area of one isosceles triangle is:
Area of one triangle = (1/2) * base * height
Where:
- Base: The length of one side of the decagon (s).
- Height: The apothem (a).
Total Area = 10 * Area of one triangle = 10 * (1/2) * s * a
This method highlights the fundamental geometric decomposition approach for finding areas of complex shapes.
Methods for Calculating the Area of an Irregular Decagon
Calculating the area of an irregular decagon is more involved and generally requires breaking it down into smaller, simpler shapes.
Method 1: Triangulation
This is a common method for finding the area of irregular polygons. The process involves dividing the decagon into triangles using diagonals. Once you have the triangles, calculate the area of each using the formula:
Area of a triangle = (1/2) * base * height
Then, sum the areas of all the triangles to get the total area of the decagon. This method necessitates knowing the lengths of the appropriate bases and heights.
Method 2: Coordinate Geometry
If you know the coordinates of each vertex of the decagon, you can utilize the surveyor's formula or the shoelace formula. These formulas are particularly useful when dealing with polygons defined by their vertices in a coordinate system.
Shoelace Formula:
This formula efficiently calculates the area of a polygon given its vertices' coordinates (xᵢ, yᵢ):
Area = (1/2) * |(x₁y₂ + x₂y₃ + ... + xₙy₁ ) - (y₁x₂ + y₂x₃ + ... + yₙx₁)|
Where:
- (xᵢ, yᵢ) are the coordinates of the vertices, starting with one vertex and proceeding around the polygon.
- n is the number of vertices (in this case, 10).
Method 3: Numerical Integration (Advanced Method)
For extremely irregular decagons with complex shapes, numerical integration techniques can be employed. These methods involve approximating the area using numerical methods, often requiring computational software or tools. This approach is far more advanced and not typically needed for most applications.
Practical Applications and Real-World Examples
Understanding how to calculate the area of a decagon extends beyond theoretical mathematics. It finds practical applications in various fields:
-
Architecture and Engineering: Calculating floor areas, land plots, or the surface area of structural components. Decagonal designs are sometimes found in buildings and other structures.
-
Construction and Surveying: Determining land area for property valuation, construction planning, and resource management.
-
Computer Graphics and Game Development: Creating realistic models and environments that often involve polygons of various shapes, including decagons.
-
Cartography: Representing geographical regions, where irregular decagons might approximate complex land boundaries.
Tips and Tricks for Accurate Calculations
-
Precision: Use precise measurements for side lengths, apothem, and coordinates to minimize errors in your calculations.
-
Units: Maintain consistent units throughout your calculations (e.g., centimeters, meters, inches).
-
Double-check: Always double-check your work, especially when using complex formulas or breaking down the decagon into multiple smaller shapes.
-
Tools: Use calculators or computer software to assist with trigonometric calculations and coordinate geometry computations.
-
Visualization: Draw a clear diagram of the decagon to help visualize the calculations, especially for irregular decagons.
Conclusion
Calculating the area of a decagon, whether regular or irregular, is achievable with the right approach. The methods outlined above offer various strategies depending on the information available. Mastering these techniques empowers you to tackle geometric challenges effectively across various disciplines. Remember to choose the method best suited to the specific information provided, always double-check your calculations, and utilize tools to streamline the process for accuracy and efficiency. With practice and understanding, you'll become proficient in determining the area of any decagon you encounter.
Latest Posts
Latest Posts
-
How To Calculate Net Run Rate In Cricket
Apr 08, 2025
-
Convert Umol L To Mg Dl
Apr 08, 2025
-
Cuanto Es 42 Libras En Kilos
Apr 08, 2025
-
How Many Cups In 20 Ounces Of Water
Apr 08, 2025
-
How To Convert Rectangular Coordinates To Polar Coordinates
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Area Of A Decagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.