How To Find The Length Of A Rectangular Prism
Treneri
Apr 06, 2025 · 6 min read
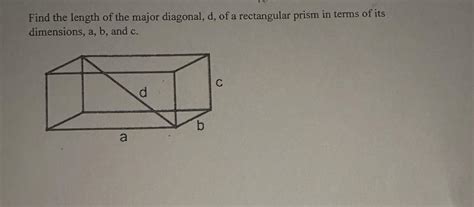
Table of Contents
How to Find the Length of a Rectangular Prism: A Comprehensive Guide
Finding the length of a rectangular prism might seem straightforward, but understanding the underlying principles and various scenarios can be surprisingly nuanced. This comprehensive guide will delve into different methods for determining the length, catering to various levels of mathematical understanding and practical situations. We'll explore scenarios where you know the volume, surface area, or even just the diagonal and other dimensions. Let's begin!
Understanding Rectangular Prisms
Before we jump into calculations, let's establish a firm grasp on what a rectangular prism is. A rectangular prism, also known as a cuboid, is a three-dimensional shape with six rectangular faces. These faces meet at right angles, forming 12 edges and 8 vertices (corners). The three dimensions defining a rectangular prism are:
- Length (l): The longest dimension of the prism.
- Width (w): The shorter dimension, often perpendicular to the length.
- Height (h): The vertical dimension, perpendicular to both length and width.
These dimensions are crucial for calculating various properties of the prism, including its volume, surface area, and diagonal length.
Method 1: Direct Measurement
The simplest method to find the length of a rectangular prism is through direct measurement. If you have a physical rectangular prism, you can use a ruler, measuring tape, or caliper to measure the length directly.
Procedure:
- Identify the longest side: Visually inspect the prism and identify the longest edge. This is the length.
- Place the measuring tool: Align the zero mark of your measuring tool with one end of the longest side.
- Measure the length: Extend the measuring tool to the opposite end of the longest side and read the measurement.
Accuracy: The accuracy of this method depends on the precision of your measuring tool. Using a calibrated measuring tool will yield the most accurate results.
Method 2: Using the Volume
If you know the volume (V) of the rectangular prism and its width (w) and height (h), you can calculate the length (l) using the following formula:
V = l * w * h
Therefore, to find the length, rearrange the formula:
l = V / (w * h)
Example:
Let's say the volume of a rectangular prism is 120 cubic centimeters, the width is 4 cm, and the height is 5 cm. Then:
l = 120 cm³ / (4 cm * 5 cm) = 120 cm³ / 20 cm² = 6 cm
The length of the rectangular prism is 6 cm.
Important Considerations: Ensure that all units are consistent (e.g., all measurements are in centimeters or all are in inches).
Method 3: Using the Surface Area
Determining the length using only the surface area requires a bit more algebraic manipulation. The surface area (SA) of a rectangular prism is given by:
SA = 2(lw + lh + wh)
Unfortunately, you cannot solve for 'l' directly from this equation without knowing at least one other dimension. This equation has three unknowns (l, w, h). To find the length, you'll need to know the surface area and at least two other dimensions (width and height). Let's demonstrate how to solve for 'l' after substituting known values.
Example:
Assume the surface area is 100 square centimeters, the width is 2 cm, and the height is 4 cm. Substitute these values into the surface area formula:
100 = 2(l2 + l4 + 2*4) 50 = 2l + 4l + 8 50 = 6l + 8 42 = 6l l = 7 cm
Therefore, the length of the rectangular prism is 7 cm.
Challenges with Surface Area: Solving for a single dimension when only the surface area is given presents multiple solutions. Additional constraints are needed for a unique solution.
Method 4: Using the Diagonal and Other Dimensions
The diagonal (d) of a rectangular prism connects two opposite corners. The relationship between the diagonal, length, width, and height is given by the Pythagorean theorem in three dimensions:
d² = l² + w² + h²
If you know the diagonal and two other dimensions, you can solve for the length:
l² = d² - w² - h²
Therefore, l = √(d² - w² - h²)
Example:
Suppose the diagonal is 13 cm, the width is 5 cm, and the height is 12 cm. Then:
l = √(13² - 5² - 12²) = √(169 - 25 - 144) = √0 = 0 cm. This doesn't make sense for a physical shape so this example isn't possible.
This reveals a critical point. The diagonal must be greater than both the width and height independently. Otherwise, the calculation results in an impossible negative number under the square root, indicating an error in the input values. Only if the diagonal measurement is greater than the combination of width and height will the result be positive.
Important Note: This formula only applies when you know the lengths of two other sides. It highlights how knowledge of other dimensions is indispensable in calculating the length from an indirect measurement like the diagonal.
Method 5: Indirect Measurement and Similar Triangles
In situations where direct measurement isn't feasible, indirect measurement techniques can be employed. If the prism casts a shadow and you know the angle of elevation of the sun and the length of the shadow, you can use trigonometry and principles of similar triangles to estimate the length.
This method involves understanding the relationship between the prism's dimensions and its shadow. Creating proportional triangles using the shadow's length and the angle of elevation allows you to calculate the unknown length of the prism. The actual calculation would depend on the specific scenario and the available information. This is a more advanced method and requires a good grasp of trigonometry.
Method 6: Using Scale Drawings or Models
If you have a scale drawing or model of the rectangular prism, you can measure the length on the drawing or model and then use the scale factor to calculate the actual length.
For example, if the scale is 1:100 and the length on the drawing is 5 cm, then the actual length is 5 cm * 100 = 500 cm. The accuracy of this method depends on the accuracy of the scale drawing or model.
Troubleshooting Common Issues
- Inconsistent Units: Ensure all your measurements are in the same units (e.g., all centimeters, all inches). Mixing units will lead to incorrect results.
- Incorrect Formula: Double-check that you are using the correct formula for the given situation.
- Measurement Errors: Measurement errors can significantly impact the accuracy of your calculations. Use precise measuring tools and measure carefully.
- Impossible Results: Negative values under a square root indicate an inconsistency in the input values. Review your measurements and calculations for errors.
Conclusion: A Multifaceted Approach
Finding the length of a rectangular prism involves a variety of techniques, each applicable in different contexts. Whether you're using direct measurement, utilizing volume or surface area calculations, employing the diagonal relationship, or resorting to indirect measurements, a thorough understanding of the fundamental principles ensures accurate and reliable results. Always remember to double-check your work and consider potential sources of error in your measurements and calculations. The choice of method depends on the information available and the required level of precision. By mastering these techniques, you'll be well-equipped to tackle various geometric challenges involving rectangular prisms.
Latest Posts
Latest Posts
-
How Long To Tan Uv 7
Apr 08, 2025
-
Cuanto Es 28 Libras En Kilos
Apr 08, 2025
-
How Much Is 60 Ml In Teaspoons
Apr 08, 2025
-
Calculadora De Asignacion De Direcciones Ipv4
Apr 08, 2025
-
How Thick Is Sheet Of Paper
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Length Of A Rectangular Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.