How To Tell If A Triangle Is Right
Treneri
Apr 07, 2025 · 6 min read
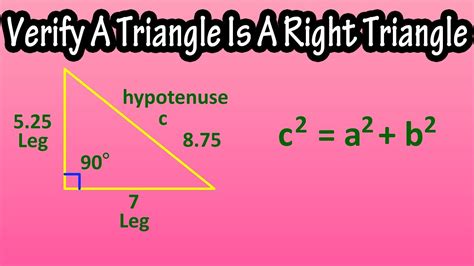
Table of Contents
How to Tell if a Triangle is a Right Triangle: A Comprehensive Guide
Determining whether a triangle is a right triangle is a fundamental concept in geometry with applications spanning various fields, from architecture and engineering to computer graphics and surveying. A right triangle, by definition, possesses one 90-degree angle (a right angle). This seemingly simple characteristic opens doors to numerous geometric theorems and problem-solving techniques. This comprehensive guide will explore multiple methods to definitively identify a right triangle, catering to various levels of mathematical understanding.
Understanding the Pythagorean Theorem: The Cornerstone of Right Triangle Identification
The Pythagorean Theorem is arguably the most famous theorem in mathematics and serves as a cornerstone for identifying right triangles. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus). Mathematically, this is represented as:
a² + b² = c²
Where:
- a and b represent the lengths of the two shorter sides (legs) of the right triangle.
- c represents the length of the hypotenuse (the longest side).
This theorem provides a powerful tool to verify if a triangle is a right triangle given the lengths of its three sides. If the equation holds true, the triangle is a right triangle; otherwise, it is not.
Applying the Pythagorean Theorem: Examples
Let's illustrate the application of the Pythagorean Theorem with a few examples:
Example 1:
Consider a triangle with sides of length 3, 4, and 5. Let's check if it's a right triangle:
3² + 4² = 9 + 16 = 25
5² = 25
Since 3² + 4² = 5², the triangle with sides 3, 4, and 5 is a right triangle. This is a classic example of a Pythagorean triple – a set of three integers that satisfy the Pythagorean Theorem.
Example 2:
Consider a triangle with sides of length 5, 12, and 13. Let's check:
5² + 12² = 25 + 144 = 169
13² = 169
Again, the equation holds true (5² + 12² = 13²), confirming that this triangle is also a right triangle. This is another example of a Pythagorean triple.
Example 3:
Now, let's consider a triangle with sides of length 2, 3, and 4. Let's see if it satisfies the Pythagorean Theorem:
2² + 3² = 4 + 9 = 13
4² = 16
Since 13 ≠ 16, the triangle with sides 2, 3, and 4 is not a right triangle.
Beyond Pythagorean Triples: Dealing with Non-Integer Side Lengths
The Pythagorean Theorem isn't limited to integer side lengths. It works equally well with decimal or fractional values. The key is to ensure accurate calculations. Consider a triangle with sides of length 2.5, 6, and 6.5:
2.5² + 6² = 6.25 + 36 = 42.25
6.5² = 42.25
Therefore, this triangle is a right triangle.
Using Trigonometric Ratios: Another Approach to Identification
Trigonometric ratios provide an alternative method for identifying right triangles, particularly when dealing with angles. The three primary trigonometric functions – sine (sin), cosine (cos), and tangent (tan) – relate the angles of a right triangle to the ratios of its sides.
- sin θ = opposite/hypotenuse
- cos θ = adjacent/hypotenuse
- tan θ = opposite/adjacent
Where θ represents an angle (other than the right angle) in the right triangle.
Applying Trigonometric Ratios: Examples
Let's explore how trigonometric ratios can help us identify right triangles:
If you know two angles of a triangle and one is 90 degrees, then it's a right triangle. If you have one angle other than the right angle, say θ, you can use the trigonometric functions to determine the lengths of the sides. For example, if you know the length of the hypotenuse and one angle, you can find the lengths of the other two sides using sine and cosine.
Similarly, if you know the length of one leg and one angle, you can use tangent to find the length of the other leg. The values obtained through these calculations will then allow you to verify the Pythagorean Theorem to confirm if it's a right triangle.
Geometric Construction and Angle Measurement: A Visual Approach
The most straightforward method to determine if a triangle is a right triangle is through direct angle measurement. Using a protractor or geometric software, measure the angles of the triangle. If one of the angles measures exactly 90 degrees, the triangle is a right triangle. This approach is particularly useful when dealing with diagrams or physical models of triangles. Accuracy in measurement is crucial here, and slight deviations from 90 degrees should be accounted for considering potential measurement errors.
Using Coordinate Geometry: Identifying Right Triangles on a Cartesian Plane
If the vertices of a triangle are represented as coordinates on a Cartesian plane, the distance formula and the slope formula can be used to determine if the triangle is a right triangle.
The Distance Formula: Calculating Side Lengths
The distance formula calculates the distance between two points (x₁, y₁) and (x₂, y₂) on a plane:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
By applying the distance formula to each pair of vertices, you can determine the lengths of the three sides of the triangle. Once you have these side lengths, you can use the Pythagorean Theorem to check if the triangle is a right triangle.
The Slope Formula: Checking for Perpendicularity
The slope formula calculates the slope (m) of a line segment connecting two points (x₁, y₁) and (x₂, y₂):
m = (y₂ - y₁)/(x₂ - x₁)
Two lines are perpendicular if the product of their slopes is -1. If two sides of the triangle are perpendicular (meaning their slopes have a product of -1), then the triangle is a right triangle.
Real-world Applications of Right Triangle Identification
Identifying right triangles is not merely an academic exercise. It has numerous practical applications:
-
Construction and Engineering: Right triangles are fundamental in structural design, ensuring stability and calculating distances and angles.
-
Navigation and Surveying: Trigonometry, heavily reliant on right triangles, is essential in determining distances, elevations, and locations.
-
Computer Graphics and Game Development: Representing and manipulating shapes in 2D and 3D graphics often utilizes the properties of right triangles.
-
Physics and Engineering: Calculations involving vectors, forces, and motion often employ the principles of right triangles.
-
Cartography and Mapmaking: Determining distances and relative positions on maps frequently involves solving right-angled triangles.
Conclusion: A Multifaceted Approach to Right Triangle Identification
Identifying a right triangle can be accomplished through multiple methods, each offering unique advantages depending on the available information. The Pythagorean Theorem provides a straightforward algebraic approach, while trigonometric ratios offer a relationship between angles and sides. Geometric construction and direct angle measurement offer a visual and intuitive approach, and coordinate geometry offers a method for analyzing triangles defined by coordinates. Understanding these diverse methods empowers you to tackle various geometrical problems effectively and appreciate the practical relevance of right triangles in diverse fields. Remember to choose the method most appropriate to the given data and context.
Latest Posts
Latest Posts
-
80 Is What Percent Of 400
Apr 09, 2025
-
Determine The Class Width Of Each Class
Apr 09, 2025
-
13 Kilometers Is How Many Miles
Apr 09, 2025
-
Cuanto Es 83 Kilos En Libras
Apr 09, 2025
-
How Much Time Until 4 30 Pm
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about How To Tell If A Triangle Is Right . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.