Is 1 4 Equivalent To 3 12
Treneri
May 13, 2025 · 5 min read
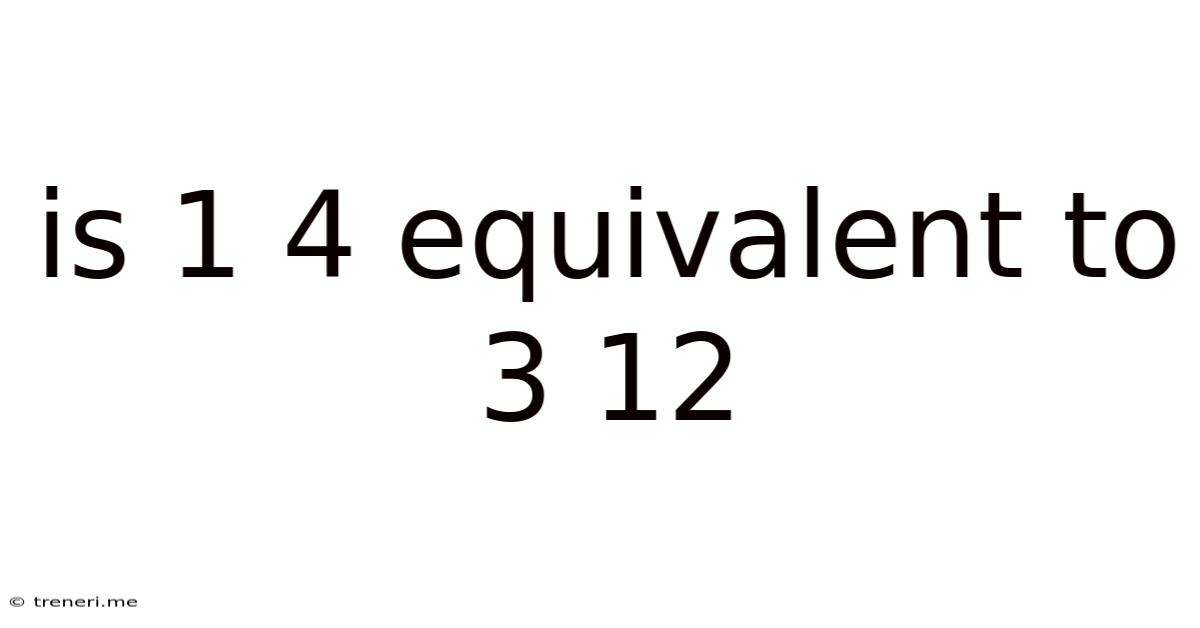
Table of Contents
Is 1/4 Equivalent to 3/12? A Deep Dive into Fraction Equivalence
Understanding fraction equivalence is fundamental to mastering arithmetic and algebra. This seemingly simple question – "Is 1/4 equivalent to 3/12?" – opens the door to a broader exploration of how fractions work, their representation, and the crucial concept of simplifying fractions to their lowest terms. This comprehensive guide will not only answer the question definitively but also equip you with the tools and understanding to tackle similar problems confidently.
What Does "Equivalent" Mean in the Context of Fractions?
Before we dive into the specifics, let's clarify what it means for two fractions to be equivalent. Two fractions are considered equivalent if they represent the same proportion or part of a whole. Even though they may look different, they represent the same value. Think of slicing a pizza: 1/4 of a pizza is the same amount as 3/12 of the same pizza, provided the pizza is divided into equal slices.
Visualizing Fraction Equivalence
A helpful way to understand equivalent fractions is through visualization. Imagine a rectangular chocolate bar.
1/4 of the Chocolate Bar:
If we divide the chocolate bar into four equal pieces, one piece represents 1/4 of the bar.
3/12 of the Chocolate Bar:
Now, imagine dividing the same chocolate bar into twelve equal pieces. Three of these smaller pieces represent 3/12 of the bar. Visually, you can see that one larger piece (1/4) is exactly the same size as three smaller pieces (3/12). This visual representation confirms their equivalence.
The Mathematical Approach: Simplifying Fractions
While visualization is helpful, the mathematical approach is crucial for solving more complex problems. The key to determining fraction equivalence lies in simplifying fractions to their lowest terms. This involves finding the greatest common divisor (GCD) of the numerator (top number) and the denominator (bottom number) and dividing both by it.
Let's simplify 3/12:
-
Find the GCD of 3 and 12: The GCD of 3 and 12 is 3 (because 3 x 1 = 3 and 3 x 4 = 12).
-
Divide both the numerator and the denominator by the GCD: 3 ÷ 3 = 1 and 12 ÷ 3 = 4.
-
Simplified Fraction: This gives us the simplified fraction 1/4.
Since simplifying 3/12 results in 1/4, we've mathematically proven that yes, 1/4 is equivalent to 3/12.
Understanding the Concept of Proportionality
The concept of equivalent fractions is intrinsically linked to proportionality. A proportion is a statement that two ratios are equal. We can express the equivalence of 1/4 and 3/12 as a proportion:
1/4 = 3/12
This means the ratio of 1 to 4 is equal to the ratio of 3 to 12. We can cross-multiply to verify this:
1 x 12 = 12 4 x 3 = 12
Since both products are equal, the proportion holds true, confirming the equivalence of the fractions.
Working with Equivalent Fractions: Real-World Applications
The ability to identify and work with equivalent fractions is essential in numerous real-world applications:
-
Cooking and Baking: Recipes often require adjusting ingredient amounts. Understanding equivalent fractions allows you to easily double, halve, or otherwise scale recipes accurately.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. The ability to convert between different fractional units (e.g., inches and feet) is vital for accuracy and safety.
-
Finance: Calculating percentages, interest rates, and proportions of budgets often involve working with fractions and their equivalents.
-
Data Analysis: Representing and interpreting data, particularly when dealing with proportions or percentages, relies heavily on the understanding of equivalent fractions.
Beyond the Basics: More Complex Fraction Equivalence Problems
While the equivalence of 1/4 and 3/12 is a straightforward example, the principles extend to more complex scenarios. Consider the following:
Is 5/15 equivalent to 1/3?
-
Find the GCD of 5 and 15: The GCD is 5.
-
Divide both the numerator and the denominator by the GCD: 5 ÷ 5 = 1 and 15 ÷ 5 = 3.
-
Simplified Fraction: This gives us 1/3.
Therefore, 5/15 is equivalent to 1/3.
Is 12/18 equivalent to 2/3?
-
Find the GCD of 12 and 18: The GCD is 6.
-
Divide both the numerator and the denominator by the GCD: 12 ÷ 6 = 2 and 18 ÷ 6 = 3.
-
Simplified Fraction: This gives us 2/3.
Therefore, 12/18 is equivalent to 2/3.
These examples demonstrate the versatility of the simplification method in determining fraction equivalence.
Troubleshooting Common Mistakes
Even with a solid understanding of the concepts, some common mistakes can arise when working with fraction equivalence:
-
Incorrectly identifying the GCD: Failing to find the greatest common divisor can lead to an incomplete simplification and an inaccurate determination of equivalence.
-
Incorrectly applying the simplification process: Dividing only the numerator or denominator, but not both, will result in an incorrect fraction.
-
Failing to simplify to the lowest terms: While a fraction might be equivalent, it's crucial to express it in its simplest form for clarity and ease of further calculations.
Conclusion: Mastering Fraction Equivalence
Understanding fraction equivalence is a cornerstone of mathematical proficiency. The ability to confidently identify and work with equivalent fractions is crucial not only for academic success but also for navigating numerous real-world applications. By mastering the techniques of simplification and proportionality, you equip yourself with a powerful tool for problem-solving and critical thinking across various disciplines. Remember the visual aids, the mathematical approach, and the real-world applications to solidify your understanding and confidently tackle any fraction equivalence challenge. The simple question, "Is 1/4 equivalent to 3/12?" has served as a springboard to exploring a much richer and more applicable mathematical concept.
Latest Posts
Latest Posts
-
How Many Hours Until May 15
May 13, 2025
-
2 X 2 3 As A Fraction
May 13, 2025
-
14 Quarts Equals How Many Gallons
May 13, 2025
-
45 Days From July 9 2024
May 13, 2025
-
Cuanto Son 58 Grados Fahrenheit En Centigrados
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1 4 Equivalent To 3 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.