Is 2 3 Equal To 4 6
Treneri
Apr 28, 2025 · 4 min read
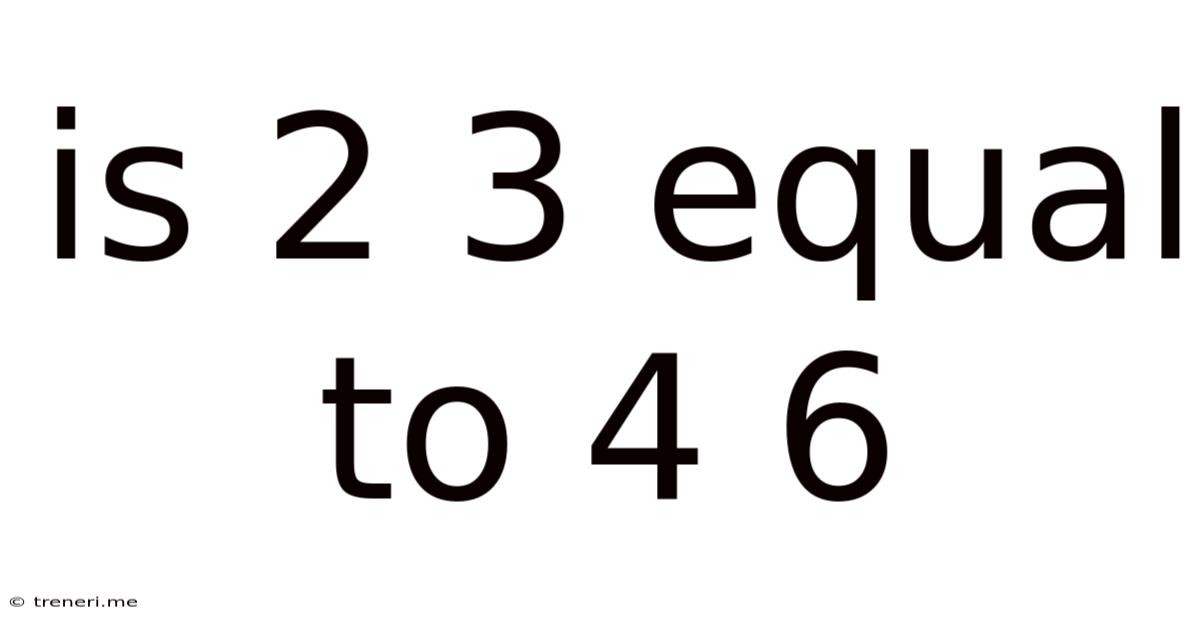
Table of Contents
Is 2/3 Equal to 4/6? A Deep Dive into Equivalent Fractions
The question, "Is 2/3 equal to 4/6?" might seem deceptively simple, especially for those comfortable with basic arithmetic. However, understanding the underlying principles behind this equivalence unlocks a deeper understanding of fractions, ratios, and their applications in various fields. This article will delve into this seemingly straightforward question, exploring the mathematical concepts involved, practical applications, and even touching upon misconceptions that might arise.
Understanding Fractions: Parts of a Whole
Before tackling the core question, let's establish a solid understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator (2) signifies that we possess two parts, while the denominator (3) indicates the whole is divided into three equal parts.
Equivalent Fractions: The Concept of Equality
Equivalent fractions represent the same proportion or value, even though they might look different. They are essentially different ways of expressing the same amount. The key to identifying equivalent fractions lies in the concept of simplification and multiplication by one.
Simplifying Fractions: Finding the Simplest Form
Simplifying a fraction involves reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This is achieved by dividing both the numerator and denominator by their greatest common divisor (GCD).
For instance, consider the fraction 4/6. Both 4 and 6 are divisible by 2. Dividing both by 2, we get:
4 ÷ 2 / 6 ÷ 2 = 2/3
This demonstrates that 4/6 simplifies to 2/3, proving they are equivalent fractions.
Multiplying by One: Expanding Fractions
Conversely, we can expand a fraction by multiplying both the numerator and denominator by the same non-zero number. This essentially multiplies the fraction by 1 (any number divided by itself equals 1), thus not changing its value.
Let's take 2/3 as an example. Multiplying both the numerator and denominator by 2:
(2 × 2) / (3 × 2) = 4/6
This shows how 2/3 can be expanded to 4/6, reinforcing their equivalence.
Visualizing Equivalence: Using Diagrams
Visual aids can greatly enhance our understanding of equivalent fractions. Imagine a pizza cut into three equal slices (representing the denominator 3). If you have two slices (numerator 2), you have 2/3 of the pizza.
Now, imagine the same pizza cut into six equal slices (denominator 6). If you have four slices (numerator 4), you still have the same amount of pizza as before – 4/6. Both scenarios represent the same proportion, visually demonstrating the equivalence of 2/3 and 4/6.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in various fields:
-
Cooking and Baking: Recipes often require adjusting ingredient quantities. If a recipe calls for 2/3 cup of sugar and you want to double the recipe, you would need to calculate the equivalent fraction of 4/6 cup, or simply 1 1/3 cups.
-
Construction and Engineering: Accurate measurements are paramount. Equivalent fractions ensure consistency and precision in projects involving ratios and proportions.
-
Finance and Accounting: Calculations involving percentages and proportions rely heavily on the concept of equivalent fractions. For example, understanding that 2/3 is equal to 66.67% allows for easier financial analysis and comparisons.
-
Data Analysis: Representing data using fractions and percentages often involves the use of equivalent fractions for better interpretation and visualization of proportions.
-
Everyday Life: Numerous everyday situations require an understanding of fractions and their equivalence. Sharing items fairly, calculating discounts, or understanding probability all involve working with fractions.
Addressing Common Misconceptions
While the concept of equivalent fractions is relatively straightforward, some misconceptions can arise:
-
Confusing Simplification with Reduction to Zero: Some might mistakenly believe that simplifying a fraction means reducing it to zero. Simplifying simply means expressing the fraction in its lowest terms, maintaining its original value.
-
Incorrect Multiplication/Division: Errors might occur when multiplying or dividing the numerator and denominator by different numbers. Remember, to maintain equivalence, both numerator and denominator must be multiplied or divided by the same non-zero number.
-
Ignoring the Whole Number Part: When dealing with mixed numbers (a combination of a whole number and a fraction), errors can occur if the whole number part isn't considered correctly when converting to improper fractions (a fraction where the numerator is greater than or equal to the denominator).
Conclusion: The Importance of Understanding Equivalence
The seemingly simple question, "Is 2/3 equal to 4/6?" opens a gateway to a deeper understanding of fractions, ratios, and their widespread applications. By grasping the concepts of simplification, multiplication by one, and visualization, we can confidently manipulate fractions and utilize them effectively in various contexts. Mastering equivalent fractions is not merely about performing calculations; it's about comprehending proportions and relationships, crucial skills applicable far beyond the realm of mathematics. The ability to recognize and work with equivalent fractions is a fundamental building block for advanced mathematical concepts and practical problem-solving in numerous fields. Therefore, a thorough understanding of this seemingly simple concept is essential for anyone seeking a strong foundation in mathematics and its diverse applications.
Latest Posts
Latest Posts
-
80 801 Rounded To The Nearest Ten Thousand
May 09, 2025
-
How Many 2x4 To Build A House
May 09, 2025
-
What Is The Quotient A 3 7 3 A 21
May 09, 2025
-
How Many Pounds Is 56 6 Liters
May 09, 2025
-
What Is 17 Degrees In Celsius
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Equal To 4 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.