Is 2 3 Equal To 8 12
Treneri
May 12, 2025 · 5 min read
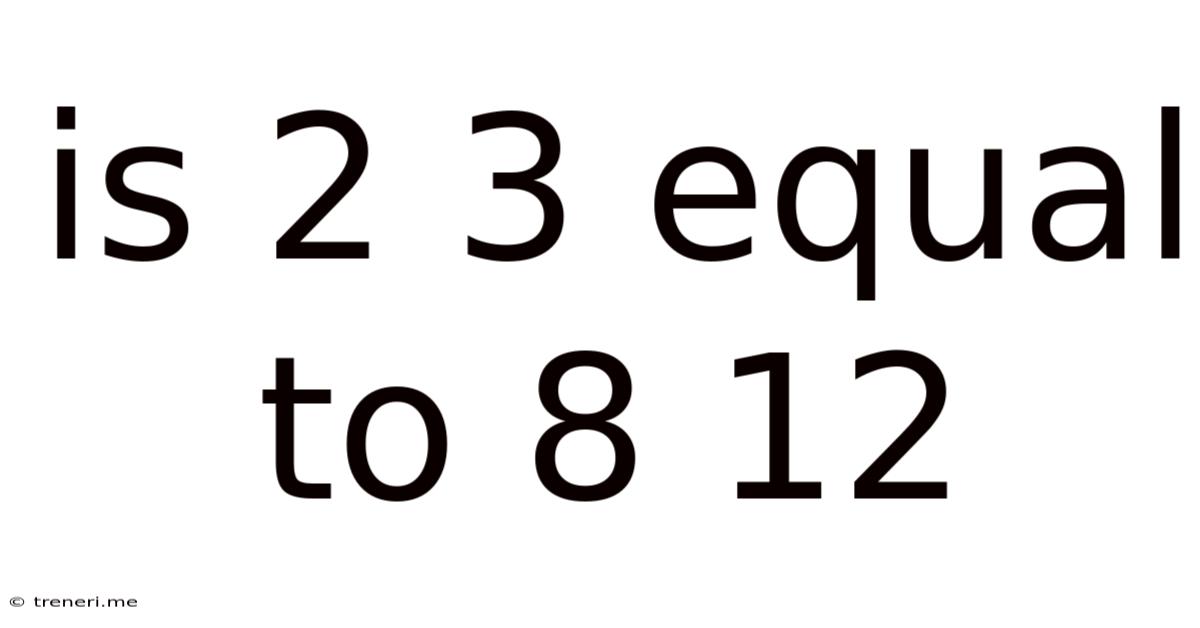
Table of Contents
Is 2/3 Equal to 8/12? A Deep Dive into Fraction Equivalence
Are the fractions 2/3 and 8/12 equal? The short answer is yes. But understanding why they are equal is crucial for grasping fundamental mathematical concepts and building a strong foundation for more advanced topics. This article will explore the concept of fraction equivalence, demonstrate why 2/3 and 8/12 are indeed equivalent, and delve into the practical applications of this knowledge.
Understanding Fractions: A Quick Refresher
Before we dive into the equivalence of 2/3 and 8/12, let's revisit the basic components of a fraction. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator (2) tells us we have two parts, and the denominator (3) tells us the whole is divided into three equal parts.
The Concept of Fraction Equivalence
Two fractions are considered equivalent if they represent the same portion of a whole, even if they look different. This means that if you visually represent both fractions, they would occupy the same area. This equivalence is achieved through a process called simplifying fractions or finding the fraction's lowest terms.
Simplifying Fractions: Finding the Lowest Terms
Simplifying a fraction involves dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's illustrate this with an example: Consider the fraction 6/9. The GCD of 6 and 9 is 3. Dividing both the numerator and denominator by 3 gives us 2/3. Therefore, 6/9 and 2/3 are equivalent fractions.
Multiplying Fractions: Creating Equivalent Fractions
Conversely, you can create equivalent fractions by multiplying both the numerator and the denominator by the same non-zero number. This process doesn't change the value of the fraction because you are essentially multiplying by 1 (in the form of a fraction like 2/2 or 3/3).
For instance, if we multiply both the numerator and denominator of 2/3 by 4, we get (2 * 4) / (3 * 4) = 8/12. This demonstrates that 2/3 and 8/12 are equivalent.
Proving the Equivalence of 2/3 and 8/12
We can definitively prove the equivalence of 2/3 and 8/12 using both simplification and multiplication:
1. Simplifying 8/12:
The GCD of 8 and 12 is 4. Dividing both the numerator and denominator by 4 gives us:
8 ÷ 4 / 12 ÷ 4 = 2/3
This clearly shows that 8/12 simplifies to 2/3, confirming their equivalence.
2. Multiplying 2/3:
As mentioned earlier, multiplying both the numerator and the denominator of a fraction by the same number creates an equivalent fraction. Multiplying 2/3 by 4/4 (which is equal to 1) gives us:
(2 * 4) / (3 * 4) = 8/12
This again proves that 2/3 and 8/12 represent the same value.
Visual Representation of Equivalence
A visual representation can solidify the understanding of fraction equivalence. Imagine a pizza cut into three equal slices. If you have two of those slices, you have 2/3 of the pizza. Now imagine the same pizza cut into twelve equal slices. Eight of those slices would represent the same amount of pizza as the two slices from the three-slice division. Both represent the same portion of the whole pizza.
Real-World Applications of Fraction Equivalence
Understanding fraction equivalence is vital in various real-world scenarios:
- Cooking and Baking: Recipes often require adjusting ingredient amounts. Knowing how to create equivalent fractions allows for accurate scaling of recipes.
- Construction and Engineering: Precise measurements are crucial. Converting between different units of measurement often involves working with equivalent fractions.
- Finance: Calculating percentages, interest rates, and proportions heavily relies on understanding and manipulating fractions.
- Data Analysis: Presenting data often involves working with proportions and percentages, which are fundamentally based on fractions.
Beyond the Basics: Working with Improper Fractions and Mixed Numbers
The principles of fraction equivalence also apply to improper fractions (where the numerator is larger than the denominator) and mixed numbers (a combination of a whole number and a fraction). For instance, the improper fraction 5/3 is equivalent to the mixed number 1 2/3, and both can be expressed as equivalent fractions like 10/6 or 15/9. Understanding how to convert between these forms and find equivalent fractions is critical for solving more complex mathematical problems.
Advanced Concepts: Ratios and Proportions
Fraction equivalence is the foundation for understanding ratios and proportions. A ratio compares two quantities, often expressed as a fraction. A proportion states that two ratios are equal. Solving proportion problems relies heavily on the ability to identify and manipulate equivalent fractions. For example, if you know that 2 out of every 3 students in a class are girls, you can use proportion to determine how many girls are in a class of 12 students.
Conclusion: Mastering Fraction Equivalence
Understanding the equivalence of fractions like 2/3 and 8/12 is not just about memorizing a fact; it's about grasping a fundamental mathematical concept that underpins many more advanced topics. The ability to simplify, multiply, and visually represent equivalent fractions is essential for success in mathematics and its numerous real-world applications. By mastering these concepts, you build a solid foundation for tackling more complex mathematical challenges and confidently navigating situations where fractions are involved. Remember, the key is to understand the underlying principle: equivalent fractions represent the same portion of a whole, regardless of their apparent differences. Practice regularly, use visual aids when needed, and you'll soon master the art of fraction equivalence.
Latest Posts
Latest Posts
-
What Is The Gcf Of 21 And 28
May 12, 2025
-
90 Days From Sep 10 2024
May 12, 2025
-
Is 1 Relatively Prime To Any Number
May 12, 2025
-
Can You Tan In 4 Uv Index
May 12, 2025
-
What Is The Gcf Of 32 And 18
May 12, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Equal To 8 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.