Is 2 A Factor Of 34
Treneri
May 09, 2025 · 5 min read
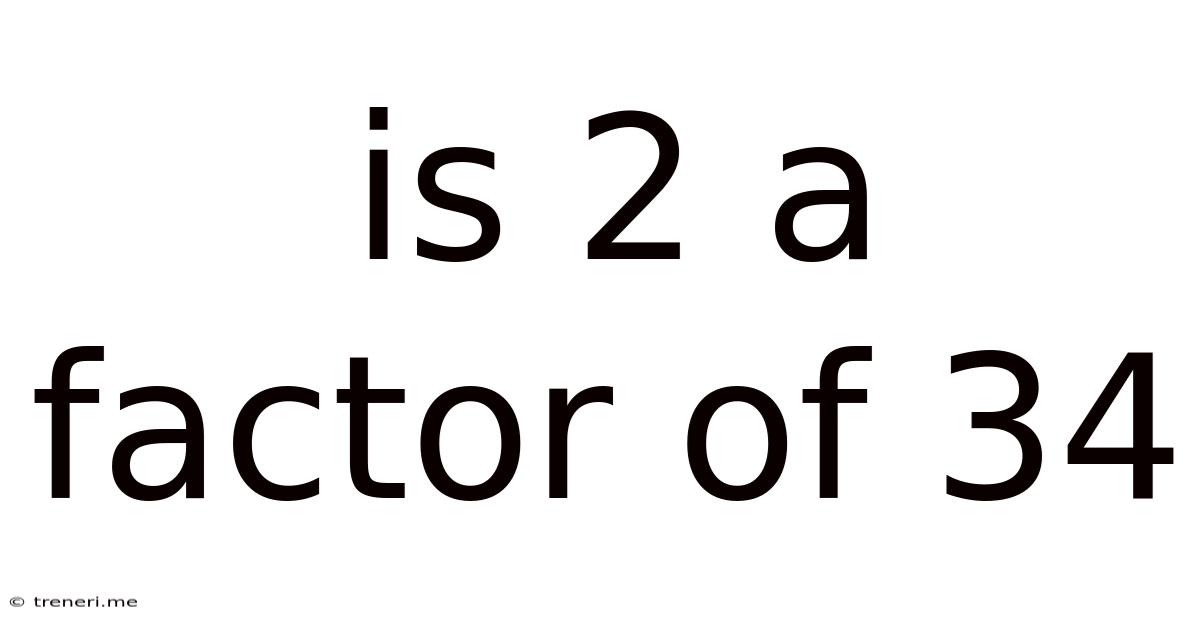
Table of Contents
Is 2 a Factor of 34? A Deep Dive into Divisibility and Factors
The seemingly simple question, "Is 2 a factor of 34?" opens a door to a fascinating exploration of fundamental mathematical concepts. While the answer itself is straightforward, understanding why it's the answer provides a strong foundation in number theory and divisibility rules. This article will delve into the question, exploring factors, divisibility, prime numbers, and even touching upon applications in more advanced mathematical fields.
Understanding Factors and Divisibility
Before we tackle the central question, let's establish a clear understanding of key terms.
What is a Factor?
A factor of a number is a whole number that divides evenly into that number without leaving a remainder. In simpler terms, if you can divide a number by another number and get a whole number result, the second number is a factor of the first. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Each of these numbers divides evenly into 12.
What is Divisibility?
Divisibility refers to the ability of one number to be divided by another number without leaving a remainder. We say that a number is divisible by another number if the division results in a whole number quotient. Divisibility rules provide shortcuts for determining if a number is divisible by certain numbers without performing the actual division.
Determining if 2 is a Factor of 34
Now, let's address the question at hand: Is 2 a factor of 34?
To determine this, we simply divide 34 by 2:
34 ÷ 2 = 17
Since the result, 17, is a whole number, we can definitively say: Yes, 2 is a factor of 34. 17 is also a factor of 34.
Divisibility Rule for 2
There's a handy divisibility rule for the number 2: A number is divisible by 2 if its last digit is an even number (0, 2, 4, 6, or 8). Since the last digit of 34 is 4 (an even number), we immediately know that 34 is divisible by 2, and therefore, 2 is a factor of 34. This rule provides a quick and efficient way to check for divisibility by 2, especially for larger numbers.
Expanding on Factors: Prime Factorization
Understanding factors leads us to the concept of prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on.
Let's find the prime factorization of 34:
- We know 2 is a factor (as we've already established).
- Dividing 34 by 2 gives us 17.
- 17 is a prime number.
Therefore, the prime factorization of 34 is 2 x 17. This representation shows all the prime numbers that, when multiplied together, equal 34. This process is crucial in various areas of mathematics, including simplifying fractions, finding greatest common divisors (GCD), and least common multiples (LCM).
Applications of Factors and Divisibility
The seemingly simple concept of factors and divisibility has far-reaching applications across numerous mathematical fields and real-world scenarios.
1. Simplifying Fractions:
When simplifying fractions, we find the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. By dividing both the numerator and denominator by the GCD, we obtain the simplest form of the fraction. Finding the GCD often involves prime factorization.
2. Solving Algebraic Equations:
Factors play a critical role in solving many algebraic equations, particularly quadratic equations. Factoring an expression involves expressing it as a product of simpler expressions. This technique allows us to find the roots (solutions) of the equation.
3. Cryptography:
Prime numbers and their properties are fundamental to modern cryptography, the science of secure communication. Many encryption algorithms rely on the difficulty of factoring large numbers into their prime factors. This inherent difficulty ensures the security of sensitive data transmitted over networks.
4. Scheduling and Calendars:
Divisibility concepts are used in creating calendars and scheduling events. Understanding the divisibility of numbers helps determine the frequency of events, such as leap years or the repetition of certain patterns.
5. Computer Science:
Factors and divisibility are important in computer algorithms and data structures. Efficient algorithms for finding factors and determining divisibility are crucial for optimizing software performance.
Beyond the Basics: Exploring Further Concepts
Let's delve slightly deeper into related mathematical concepts that build upon our understanding of factors and divisibility.
Greatest Common Divisor (GCD):
The greatest common divisor (GCD) of two or more numbers is the largest number that divides all the numbers without leaving a remainder. Finding the GCD is often facilitated by prime factorization. For example, the GCD of 34 and 51 can be found using their prime factorizations:
- 34 = 2 x 17
- 51 = 3 x 17
The GCD is 17, as it's the largest number that divides both 34 and 51.
Least Common Multiple (LCM):
The least common multiple (LCM) of two or more numbers is the smallest number that is a multiple of all the numbers. The LCM is useful in various applications, such as finding the least common denominator when adding or subtracting fractions.
Modular Arithmetic:
Modular arithmetic, also known as clock arithmetic, deals with remainders after division. It's a powerful tool used in cryptography and computer science. The concept of divisibility is fundamental to understanding modular arithmetic.
Conclusion: The Significance of a Simple Question
The seemingly simple question, "Is 2 a factor of 34?", serves as a springboard for exploring a vast landscape of mathematical concepts. From basic divisibility rules to advanced cryptographic applications, the understanding of factors and divisibility is essential across many areas of mathematics and beyond. By understanding these fundamental concepts, we gain a deeper appreciation for the interconnectedness of mathematical ideas and their practical implications in the world around us. The answer, yes, is only the beginning of a rich and rewarding journey into the world of numbers.
Latest Posts
Latest Posts
-
5 Is 1 Of What Number
May 10, 2025
-
What Is The Measure Of 44 50 64 92
May 10, 2025
-
How Many Days Is In Two Months
May 10, 2025
-
How Long Till 5 Pm Today
May 10, 2025
-
How To Find The Base Of Triangular Prism
May 10, 2025
Related Post
Thank you for visiting our website which covers about Is 2 A Factor Of 34 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.