Is 2 A Factor Of 73
Treneri
May 15, 2025 · 5 min read
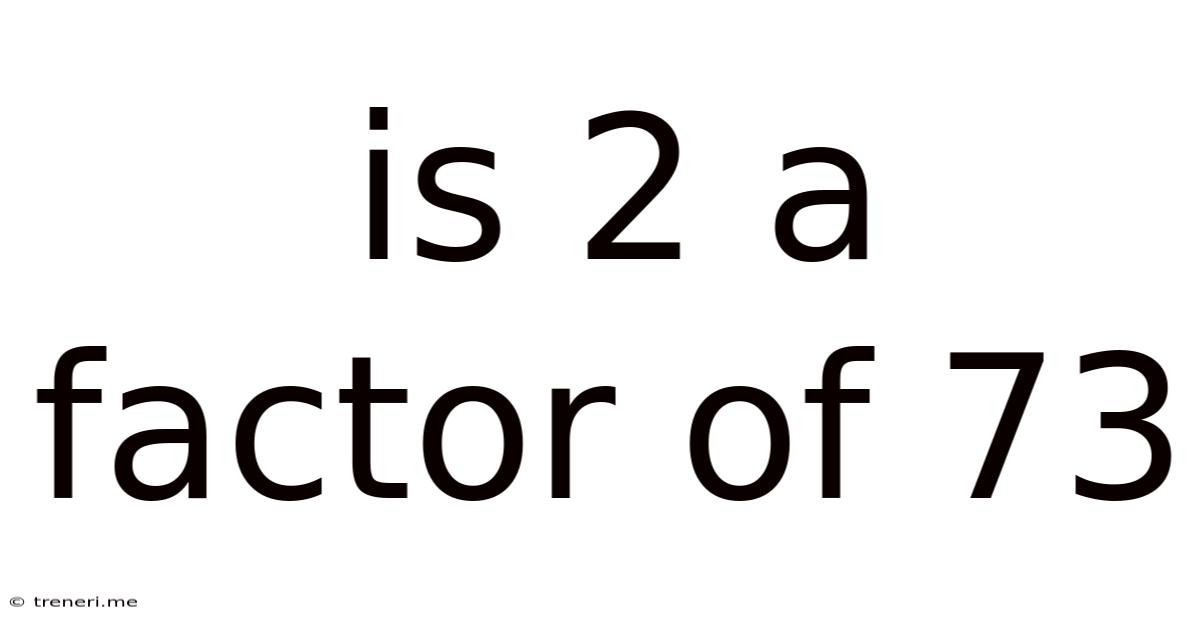
Table of Contents
Is 2 a Factor of 73? A Deep Dive into Divisibility and Prime Numbers
The seemingly simple question, "Is 2 a factor of 73?" opens a door to a fascinating exploration of number theory, divisibility rules, and the properties of prime numbers. While the answer itself is straightforward, understanding why it's the answer provides a valuable foundation in mathematical concepts. This article will not only answer the question definitively but also delve into the underlying principles, offering a comprehensive understanding for both beginners and those seeking a refresher.
Understanding Factors and Divisibility
Before tackling the specific question, let's establish a clear understanding of key terms. A factor (or divisor) of a number is a whole number that divides the number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Divisibility, in simple terms, refers to whether one number can be divided by another number without leaving a remainder. We often use divisibility rules as shortcuts to determine divisibility without performing the actual division. These rules are especially useful for larger numbers.
Divisibility Rules: A Quick Refresher
Several divisibility rules exist for various numbers. The rule for divisibility by 2 is particularly relevant to our question:
- Divisibility by 2: A number is divisible by 2 if its last digit is an even number (0, 2, 4, 6, or 8).
This rule is based on the structure of the decimal number system. Since any number can be expressed as a sum of powers of 10 (e.g., 123 = 100 + 20 + 3), and all even powers of 10 are divisible by 2, the divisibility of the entire number depends only on the last digit.
Applying the Divisibility Rule to 73
Now, let's apply the divisibility rule by 2 to the number 73. The last digit of 73 is 3, which is an odd number. Therefore, according to the divisibility rule, 73 is not divisible by 2. This means 2 is not a factor of 73.
The Significance of Prime Numbers
The fact that 2 is not a factor of 73 also relates to the concept of prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime numbers are the building blocks of all other whole numbers through a process called prime factorization.
73 is a prime number because its only divisors are 1 and 73. Prime numbers are inherently indivisible by any whole number other than 1 and themselves. Since 2 is a whole number other than 1 and 73, it cannot be a factor of 73. This reinforces our conclusion drawn from the divisibility rule.
Exploring Other Divisibility Rules (Beyond the Scope of the Main Question)
While the divisibility rule for 2 directly answers our question, let's briefly explore other divisibility rules to enhance our understanding of number theory:
-
Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. For example, 123 is divisible by 3 because 1 + 2 + 3 = 6, which is divisible by 3.
-
Divisibility by 4: A number is divisible by 4 if the number formed by its last two digits is divisible by 4. For example, 1236 is divisible by 4 because 36 is divisible by 4.
-
Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
-
Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
-
Divisibility by 10: A number is divisible by 10 if its last digit is 0.
These rules provide efficient ways to determine divisibility without lengthy calculations, particularly useful when dealing with larger numbers.
Prime Factorization and its Relationship to Factors
Prime factorization is the process of expressing a whole number as a product of its prime factors. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). Every whole number greater than 1 can be uniquely expressed as a product of prime numbers.
Since 73 is a prime number, its prime factorization is simply 73. This confirms that its only factors are 1 and 73. The absence of 2 in its prime factorization definitively shows that 2 is not a factor of 73.
Practical Applications and Real-World Examples
Understanding factors and divisibility has practical applications in various fields:
-
Computer Science: Divisibility and prime numbers are fundamental in cryptography, ensuring data security and encryption.
-
Engineering: Divisibility is crucial in designing structures and systems, ensuring optimal resource allocation and efficiency.
-
Everyday Life: Divisibility helps in everyday tasks like sharing items equally among a group of people or calculating quantities.
Conclusion: A Definitive Answer and Broader Implications
To reiterate, the answer to the question "Is 2 a factor of 73?" is a definitive no. This is evident through both the divisibility rule for 2 and the fact that 73 is a prime number. Exploring this seemingly simple question has allowed us to delve into the fundamental concepts of factors, divisibility, prime numbers, and prime factorization. These mathematical principles have widespread applications, showcasing the interconnectedness of seemingly disparate fields and the practical value of understanding basic number theory. The seemingly simple question has revealed a rich tapestry of mathematical concepts, highlighting the beauty and utility of mathematics in our world. The exploration goes beyond simply answering the question; it lays a solid foundation for deeper understanding and appreciation of the number system.
Latest Posts
Latest Posts
-
Qual A Diferenca De Libra Para Quilo
May 15, 2025
-
26 Out Of 30 Letter Grade
May 15, 2025
-
Before A Sale An Items Price Was 18 00
May 15, 2025
-
1 Divided By The Square Root Of 2
May 15, 2025
-
Which Square Root Is Between 4 And 5
May 15, 2025
Related Post
Thank you for visiting our website which covers about Is 2 A Factor Of 73 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.