Is 3 A Factor Of 75
Treneri
May 12, 2025 · 5 min read
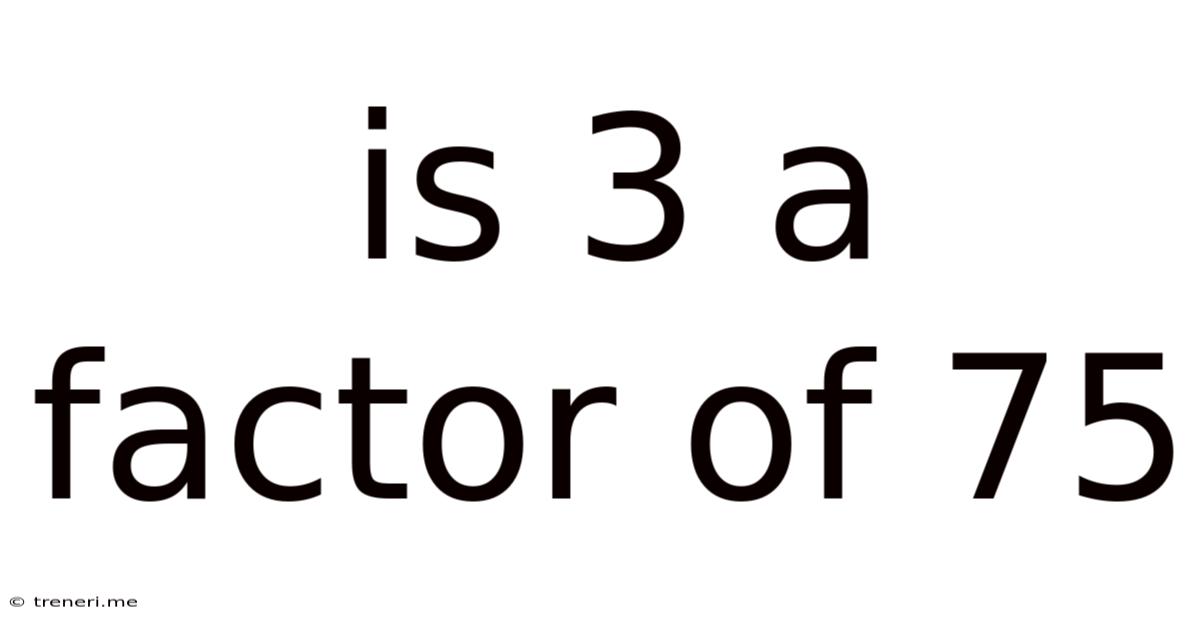
Table of Contents
Is 3 a Factor of 75? A Deep Dive into Divisibility and Factors
The question, "Is 3 a factor of 75?" might seem simple at first glance. For those comfortable with basic arithmetic, the answer is a straightforward yes. However, exploring this seemingly simple question opens the door to a fascinating world of mathematical concepts like divisibility rules, prime factorization, and the fundamental theorem of arithmetic. This article will not only answer the question definitively but also delve into the underlying principles, providing a comprehensive understanding of factors and divisibility.
Understanding Factors and Divisibility
Before we tackle the specific question about 75, let's establish a clear understanding of the key terms.
Factors: A factor of a number is a whole number that divides the number exactly, leaving no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Each of these numbers divides 12 without leaving any remainder.
Divisibility: Divisibility refers to the ability of one number to be divided by another without leaving a remainder. We say that a number is divisible by another if the result of the division is a whole number. For instance, 12 is divisible by 3 because 12 ÷ 3 = 4 (a whole number).
Prime Numbers: Prime numbers are whole numbers greater than 1 that have only two factors: 1 and themselves. Examples include 2, 3, 5, 7, 11, and so on. Prime numbers are the building blocks of all other whole numbers.
Composite Numbers: Composite numbers are whole numbers greater than 1 that have more than two factors. For example, 12 is a composite number because it has factors 1, 2, 3, 4, 6, and 12.
The Divisibility Rule for 3
A crucial tool for determining divisibility by 3 is the divisibility rule for 3. This rule states:
A number is divisible by 3 if the sum of its digits is divisible by 3.
Let's apply this rule to various numbers:
- 12: The sum of the digits (1 + 2 = 3) is divisible by 3, so 12 is divisible by 3.
- 27: The sum of the digits (2 + 7 = 9) is divisible by 3, so 27 is divisible by 3.
- 45: The sum of the digits (4 + 5 = 9) is divisible by 3, so 45 is divisible by 3.
- 114: The sum of the digits (1 + 1 + 4 = 6) is divisible by 3, so 114 is divisible by 3.
Is 3 a Factor of 75? Applying the Divisibility Rule
Now, let's apply the divisibility rule for 3 to the number 75:
- Sum the digits: 7 + 5 = 12
- Check for divisibility by 3: 12 is divisible by 3 (12 ÷ 3 = 4).
Therefore, since the sum of the digits of 75 is divisible by 3, 75 itself is divisible by 3. This means that 3 is a factor of 75.
Further Exploring Factors of 75: Prime Factorization
We can further solidify our understanding by performing prime factorization of 75. Prime factorization is the process of expressing a composite number as a product of its prime factors.
75 can be factored as follows:
75 = 3 × 25
Since 25 is not a prime number, we can further factor it:
25 = 5 × 5
Therefore, the prime factorization of 75 is:
75 = 3 × 5 × 5 or 3 × 5²
This clearly shows that 3 is one of the prime factors of 75, confirming that 3 is indeed a factor of 75. The prime factorization method provides a more rigorous approach to identifying factors, particularly for larger numbers.
The Fundamental Theorem of Arithmetic
The process of prime factorization is directly related to the Fundamental Theorem of Arithmetic. This theorem states that every whole number greater than 1 can be uniquely expressed as a product of prime numbers (ignoring the order of the factors). This uniqueness is crucial in mathematics, allowing us to definitively identify the factors of any number. The prime factorization of 75 illustrates this theorem perfectly.
Practical Applications of Divisibility and Factors
Understanding divisibility and factors is not just an academic exercise. These concepts have numerous practical applications across various fields:
-
Simplification of Fractions: Finding common factors allows us to simplify fractions to their lowest terms. For example, simplifying 75/150 involves finding the greatest common factor (GCF) of 75 and 150, which is 75. Therefore, 75/150 simplifies to 1/2.
-
Measurement and Division: Divisibility is critical in scenarios involving measurement and division. For example, if you have 75 meters of rope and need to cut it into 3-meter pieces, you can easily determine that you'll have 25 pieces.
-
Algebra and Equation Solving: Factorization is a fundamental technique in algebra for solving equations and simplifying expressions.
-
Computer Science and Cryptography: Prime factorization is essential in cryptography, forming the basis of many encryption algorithms.
Conclusion: Beyond a Simple "Yes"
The answer to the question "Is 3 a factor of 75?" is undoubtedly yes. However, exploring this question allowed us to delve deeper into the core concepts of divisibility, factors, prime factorization, and the fundamental theorem of arithmetic. These concepts are fundamental to various mathematical fields and have practical applications in everyday life and various professional contexts. By understanding these principles, we gain a more profound appreciation for the elegance and power of mathematics. The seemingly simple question of the divisibility of 75 by 3 serves as a gateway to a rich and rewarding mathematical journey.
Latest Posts
Latest Posts
-
How Much Hours Until 6 Am
May 13, 2025
-
1 Inch Of Rain Is Equivalent To How Much Snow
May 13, 2025
-
4 5 As An Improper Fraction
May 13, 2025
-
1994 How Old Am I 2024
May 13, 2025
-
How Many Mm In 9 Cm
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 3 A Factor Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.