Is 8 10 Equivalent To 4 5
Treneri
May 14, 2025 · 5 min read
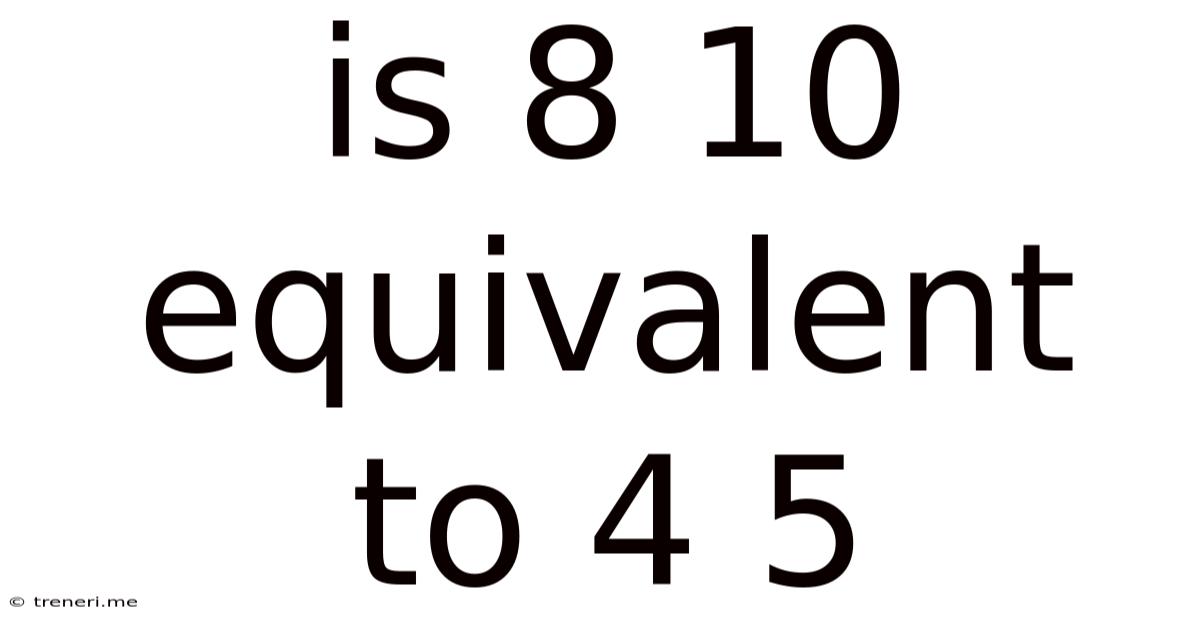
Table of Contents
Is 8:10 Equivalent to 4:5? A Deep Dive into Ratio and Proportion
The question, "Is 8:10 equivalent to 4:5?" might seem simple at first glance. However, understanding the underlying principles of ratios and proportions is crucial not just for answering this specific question but also for tackling a wide range of mathematical problems in various fields, from cooking and construction to finance and engineering. This article will explore the concept of equivalent ratios, demonstrating how to determine equivalence, and exploring the broader implications of this fundamental mathematical relationship.
Understanding Ratios
A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. Ratios can be expressed in several ways:
- Using a colon: 8:10
- As a fraction: 8/10
- Using the word "to": 8 to 10
In the context of our question, 8:10 represents a ratio where there are 8 units of one quantity for every 10 units of another.
Understanding Proportions
A proportion states that two ratios are equal. It's a statement of equality between two ratios. For example, if we have two ratios, a:b and c:d, a proportion would be written as:
a/b = c/d or a:b = c:d
To determine if two ratios are proportional, we need to check if they simplify to the same ratio in their simplest form.
Simplifying Ratios
Simplifying a ratio involves finding the greatest common divisor (GCD) of the two numbers and dividing both by it. This process reduces the ratio to its simplest form, making comparisons easier.
Let's simplify the ratio 8:10:
The GCD of 8 and 10 is 2. Dividing both numbers by 2, we get:
8 ÷ 2 = 4 10 ÷ 2 = 5
Therefore, the simplified ratio is 4:5.
Determining Equivalence: Is 8:10 Equivalent to 4:5?
Now, we can directly answer the initial question. Since simplifying the ratio 8:10 gives us 4:5, the answer is a resounding yes. The ratios 8:10 and 4:5 are equivalent. They represent the same relative relationship between two quantities.
Methods for Checking Ratio Equivalence
Beyond simplification, there are other ways to check if two ratios are equivalent:
1. Cross-Multiplication:
This method involves multiplying the numerator of one ratio by the denominator of the other and vice versa. If the products are equal, the ratios are equivalent.
For 8:10 and 4:5:
8 * 5 = 40 10 * 4 = 40
Since both products are equal, the ratios are equivalent.
2. Converting to Decimals:
Converting each ratio to a decimal allows for direct comparison.
8/10 = 0.8 4/5 = 0.8
Since both ratios equal 0.8, they are equivalent.
Real-World Applications of Equivalent Ratios
Understanding equivalent ratios is essential in many practical applications:
-
Scaling Recipes: If a recipe calls for a 2:1 ratio of flour to sugar, you can easily scale it up or down using equivalent ratios. A doubled recipe would maintain the 2:1 ratio, perhaps using 4 cups of flour to 2 cups of sugar.
-
Map Scales: Maps use ratios to represent distances. A scale of 1:100,000 means that 1 unit on the map represents 100,000 units in reality. Equivalent ratios are used to calculate distances on the map corresponding to real-world distances.
-
Unit Conversion: Converting units (e.g., kilometers to miles, liters to gallons) often involves using equivalent ratios. Conversion factors are essentially equivalent ratios.
-
Financial Ratios: In finance, various ratios (like debt-to-equity ratio or profit margin) are used to analyze a company's financial health. Understanding equivalent ratios helps in comparing companies of different sizes.
-
Mixing Solutions: In chemistry and other scientific fields, precise ratios are crucial for mixing solutions. Equivalent ratios ensure the correct concentration is achieved regardless of the total volume.
-
Construction and Engineering: Blueprints and architectural drawings use ratios to represent real-world dimensions. Ensuring accurate scaling relies heavily on the understanding of equivalent ratios and proportions.
Beyond Simple Ratios: Extending the Concept
While the example of 8:10 and 4:5 involves simple whole numbers, the concept of equivalent ratios extends to more complex scenarios involving decimals, fractions, and even algebraic expressions. The fundamental principles remain the same: equivalent ratios represent the same relative relationship between quantities.
For instance, consider the ratios 0.5:1 and 5:10. While these involve decimals, they simplify to the equivalent ratio 1:2. Similarly, algebraic expressions can form ratios; determining equivalence involves similar techniques, often employing algebraic manipulation to simplify the expressions.
Common Mistakes to Avoid
Several common mistakes can arise when working with ratios and proportions:
-
Incorrect Simplification: Failing to find the greatest common divisor leads to incomplete simplification, making comparisons inaccurate.
-
Confusion with Fractions: While ratios are closely related to fractions, they are not always treated identically. The context is crucial. A fraction represents a part of a whole, while a ratio represents a comparison between two or more quantities.
-
Incorrect Cross-Multiplication: Errors in performing cross-multiplication can lead to incorrect conclusions about equivalence. Care must be taken to multiply correctly.
-
Ignoring Units: In real-world applications, units are critical. Failing to account for units can lead to significant errors in calculations and interpretations.
Conclusion
The question "Is 8:10 equivalent to 4:5?" serves as a gateway to understanding the fundamental concepts of ratios and proportions. The answer, a definitive "yes," underscores the importance of simplifying ratios to their simplest form for accurate comparison. The ability to determine equivalence is crucial in numerous fields, highlighting the practical significance of this seemingly simple mathematical concept. By mastering these principles and avoiding common errors, one can confidently navigate various mathematical problems involving ratios and proportions, contributing to success in academic and professional endeavors. Through understanding and applying these methods, one can gain a deeper comprehension of mathematical relationships and their relevance to real-world applications.
Latest Posts
Latest Posts
-
Can I Get Tan In Uv 5
May 14, 2025
-
500 Miles Equals How Many Kilometers
May 14, 2025
-
Does Elbow Macaroni Double In Size When Cooked
May 14, 2025
-
Cuanto Es El 10 De 200
May 14, 2025
-
How Long Is 65 Days In Months
May 14, 2025
Related Post
Thank you for visiting our website which covers about Is 8 10 Equivalent To 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.