Lcm Of 10 5 And 3
Treneri
May 12, 2025 · 4 min read
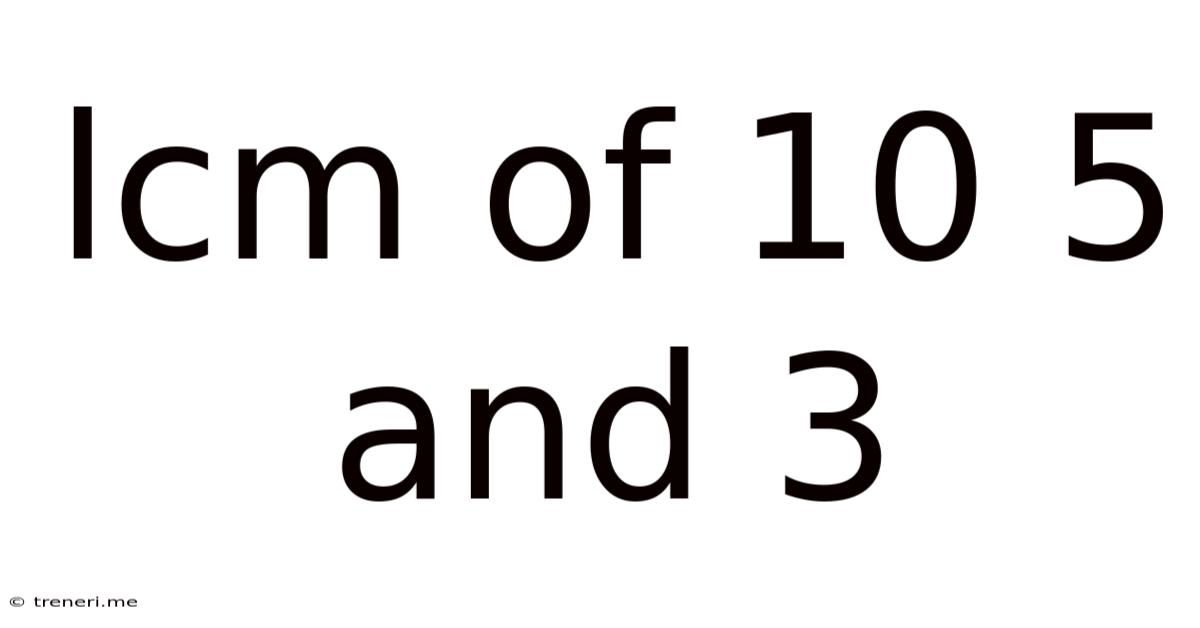
Table of Contents
Finding the LCM of 10, 5, and 3: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex scheduling problems. This article will delve into the process of calculating the LCM of 10, 5, and 3, exploring various methods and highlighting their practical significance. We'll also touch upon the broader context of LCM within number theory and its real-world applications.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 10, 5, and 3, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Calculating LCM
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. The most common methods are:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. You simply list the multiples of each number until you find the smallest common multiple.
Let's apply this to our example:
- Multiples of 10: 10, 20, 30, 40, 50, 60...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The smallest number appearing in all three lists is 30. Therefore, the LCM of 10, 5, and 3 is 30.
This method is simple to understand but becomes less efficient with larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Let's break down the prime factorization of each number:
- 10 = 2 × 5
- 5 = 5
- 3 = 3
Now, we identify the highest power of each prime factor present:
- 2¹ (from 10)
- 5¹ (from 10 and 5)
- 3¹ (from 3)
To find the LCM, we multiply these highest powers together:
LCM(10, 5, 3) = 2¹ × 5¹ × 3¹ = 30
This method is more systematic and generally faster than listing multiples, especially for larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) are closely related. The relationship is expressed by the following formula:
LCM(a, b) × GCD(a, b) = a × b
This can be extended to more than two numbers. While finding the GCD might seem like an extra step, it can be more efficient than prime factorization for some numbers, especially if you're already familiar with GCD calculation methods like the Euclidean algorithm.
Applying the LCM: Real-World Examples
The LCM has numerous practical applications in various fields:
1. Scheduling Problems
Imagine you have three machines that perform different tasks in a production line. Machine A completes its cycle every 10 minutes, Machine B every 5 minutes, and Machine C every 3 minutes. To determine when all three machines will be simultaneously at the beginning of their cycle, you need to find the LCM(10, 5, 3) = 30. This means all three machines will align at the start of their cycles every 30 minutes.
2. Fraction Addition and Subtraction
To add or subtract fractions with different denominators, you need to find a common denominator. The LCM of the denominators is the most efficient common denominator.
3. Music Theory
The LCM is used in music theory to determine the least common multiple of note durations or rhythmic patterns, helping musicians create harmonious compositions.
4. Cyclic Processes
In many systems involving cyclical processes (e.g., planetary orbits, repeating events), the LCM can help predict when the cycles will coincide.
Beyond the Basics: Extending LCM Concepts
The concept of LCM extends beyond integers to other mathematical structures. For instance, you can find the LCM of polynomials. Understanding the LCM and its various computational methods is crucial for progressing to more advanced mathematical concepts.
Conclusion
Finding the LCM of 10, 5, and 3, as demonstrated above, highlights the fundamental importance of this mathematical concept. Whether using the listing multiples, prime factorization, or GCD method, the result remains the same: 30. Understanding the different methods and their applications allows for efficient problem-solving in various contexts, ranging from simple scheduling issues to more complex mathematical endeavors. The practical applications of the LCM span numerous fields, showcasing its relevance beyond theoretical mathematics. By mastering the concepts of LCM and its related GCD, you enhance your mathematical toolkit and gain a deeper appreciation for the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
How Many Calories Do I Burn Pumping
May 14, 2025
-
10 Ml Is The Same As
May 14, 2025
-
How Many Cups In 96 Oz
May 14, 2025
-
What Grade Is A 12 Out Of 18
May 14, 2025
-
What Is An 80 Out Of 100
May 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 5 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.