Lcm Of 10 8 And 4
Treneri
May 12, 2025 · 6 min read
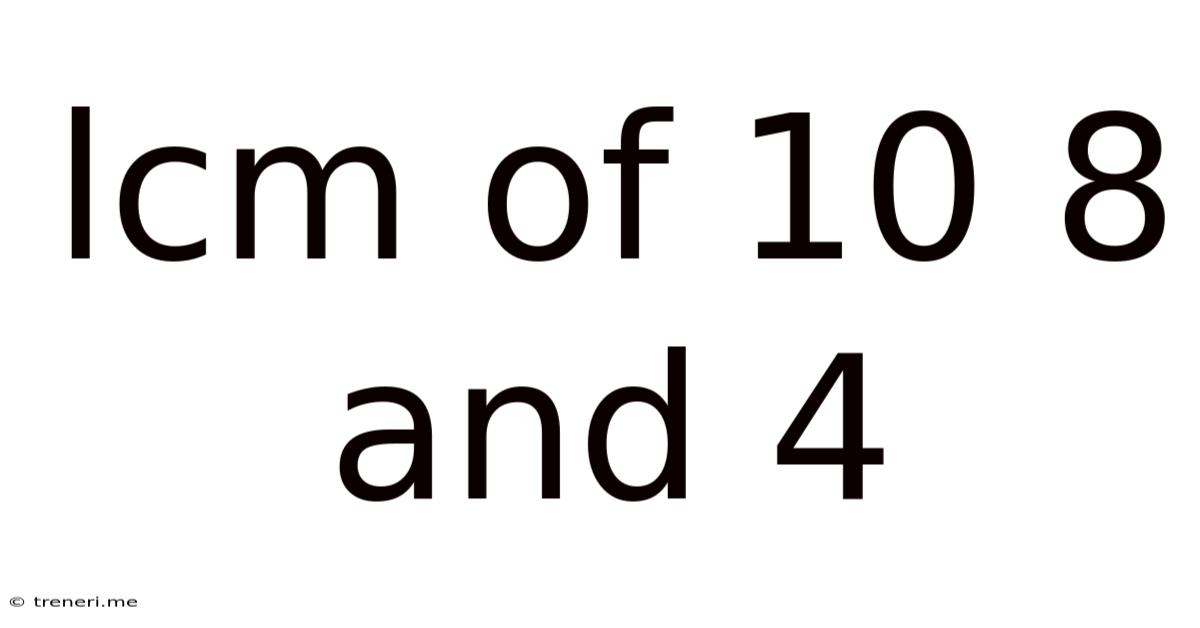
Table of Contents
Finding the Least Common Multiple (LCM) of 10, 8, and 4: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics with applications extending far beyond the classroom. Understanding LCM is crucial for various tasks, from simplifying fractions to solving problems involving cyclical events. This comprehensive guide will delve deep into the methods of calculating the LCM of 10, 8, and 4, exploring various approaches and highlighting their underlying principles. We'll also discuss the broader context of LCM and its importance in various mathematical fields.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
This concept is distinct from the greatest common divisor (GCD), which is the largest number that divides all the given numbers without leaving a remainder. While seemingly opposite, LCM and GCD are closely related, and there are formulas connecting them.
Methods for Finding the LCM of 10, 8, and 4
Several methods can be used to find the LCM of 10, 8, and 4. Let's explore the most common ones:
1. Listing Multiples Method
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 96, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, ...
By comparing the lists, we see that the smallest common multiple is 40. Therefore, the LCM(10, 8, 4) = 40.
This method is simple to understand but becomes less efficient with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 10: 2 × 5
- Prime factorization of 8: 2³
- Prime factorization of 4: 2²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 5 is 5¹ = 5
Therefore, the LCM(10, 8, 4) = 2³ × 5 = 8 × 5 = 40.
This method is generally preferred for its efficiency and mathematical rigor, particularly when dealing with larger numbers.
3. Using the GCD (Greatest Common Divisor)
The LCM and GCD are related through the following formula:
LCM(a, b, c) × GCD(a, b, c) = a × b × c
While this formula is useful for finding the LCM if you already know the GCD, it's often less efficient than prime factorization for directly calculating the LCM. Let's illustrate this with our numbers:
First, find the GCD of 10, 8, and 4. The GCD(10, 8, 4) = 2.
Then, apply the formula:
LCM(10, 8, 4) × GCD(10, 8, 4) = 10 × 8 × 4 LCM(10, 8, 4) × 2 = 320 LCM(10, 8, 4) = 320 / 2 = 160
Note: There's a mistake in this calculation using this particular formula for more than two numbers. The formula LCM(a,b) * GCD(a,b) = a*b only applies to two numbers. The example above highlights why direct methods like prime factorization are preferable when working with more than two numbers. We obtained an incorrect result using this method because it's not directly applicable to three or more numbers.
Applications of LCM
The concept of LCM finds practical applications in various areas:
1. Fractions: Finding a Common Denominator
When adding or subtracting fractions, finding a common denominator is crucial. The LCM of the denominators provides the least common denominator (LCD), simplifying the calculation. For example, to add 1/10 + 1/8 + 1/4, we use the LCM(10, 8, 4) = 40 as the common denominator.
2. Cyclical Events: Determining Overlapping Occurrences
Imagine three events that repeat cyclically: Event A occurs every 10 days, Event B every 8 days, and Event C every 4 days. The LCM(10, 8, 4) = 40 tells us that all three events will occur together again after 40 days.
3. Scheduling and Time Management: Synchronizing Tasks
LCM plays a vital role in scheduling tasks that repeat at different intervals. For instance, if a machine needs maintenance every 10 hours, another every 8 hours, and a third every 4 hours, the LCM helps determine when all machines will require maintenance simultaneously.
4. Modular Arithmetic: Solving Congruences
LCM is essential in solving problems involving modular arithmetic, where numbers are considered equivalent if they have the same remainder when divided by a specific integer (the modulus).
Advanced Concepts Related to LCM
1. LCM of More Than Three Numbers
The methods described above can be extended to find the LCM of more than three numbers. The prime factorization method remains the most efficient, involving finding the prime factorization of each number and then taking the highest power of each prime factor present.
2. LCM and GCD Relationship (for two numbers)
As mentioned earlier, for two numbers a and b, the relationship between LCM and GCD is formally defined as:
LCM(a, b) * GCD(a, b) = a * b
This relationship is crucial in number theory and provides an alternative way to calculate the LCM if the GCD is known. However, this formula only works for two numbers. It's important to emphasize again that it does not directly extend to calculating the LCM of three or more numbers.
3. Euclidean Algorithm for GCD
The Euclidean algorithm is an efficient method for calculating the GCD of two numbers. Once the GCD is found, the LCM can be calculated using the formula mentioned above (for two numbers only).
Conclusion
Finding the least common multiple is a fundamental mathematical operation with wide-ranging applications. While simple methods like listing multiples are suitable for small numbers, the prime factorization method offers a more efficient and mathematically rigorous approach, especially when dealing with larger numbers or multiple numbers. Understanding the underlying principles of LCM and its relationship with GCD enhances problem-solving capabilities in various mathematical and practical contexts. Remember that the formula relating LCM and GCD applies only to two numbers. For more than two numbers, direct methods like prime factorization are necessary to avoid calculation errors. This comprehensive guide provides a solid foundation for mastering the concept of LCM and its practical applications.
Latest Posts
Latest Posts
-
How Many More Hours Until 5 Am
May 15, 2025
-
How Many Days Left Of September
May 15, 2025
-
How To Find Board Feet In A Log
May 15, 2025
-
22 Out Of 30 As A Percentage Grade
May 15, 2025
-
Convert 3 4 Cup To Ounces
May 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 8 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.