Lcm Of 2 4 And 5
Treneri
May 11, 2025 · 5 min read
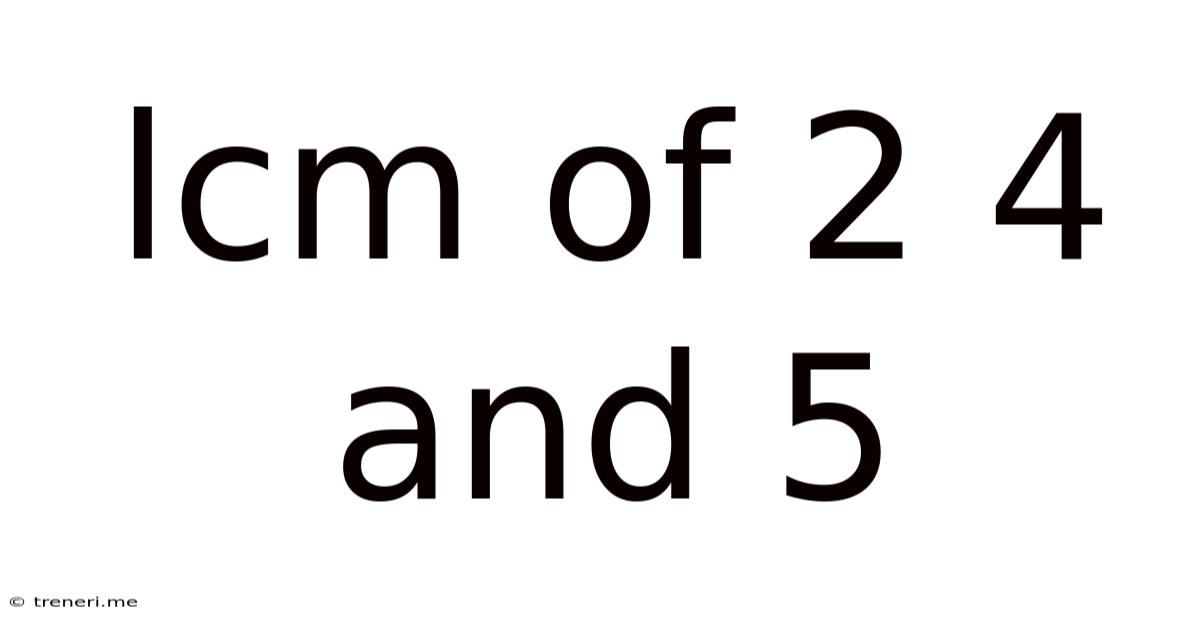
Table of Contents
Finding the Least Common Multiple (LCM) of 2, 4, and 5: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in various fields like fractions, scheduling, and even music theory. This article delves deep into calculating the LCM of 2, 4, and 5, explaining multiple methods and showcasing their applications. We'll explore different approaches, highlighting their strengths and weaknesses, to ensure a complete understanding of this important mathematical operation.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 2, 4, and 5, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Calculating LCM
Several methods exist for calculating the LCM of a set of numbers. We will explore three common methods, focusing on their application to find the LCM of 2, 4, and 5:
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40...
By comparing the lists, we can see that the smallest common multiple of 2, 4, and 5 is 20.
Advantages: Simple and easy to understand, particularly suitable for small numbers.
Disadvantages: Becomes inefficient and time-consuming for larger numbers or a greater number of integers.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. The LCM is then constructed by taking the highest power of each prime factor present in the numbers.
Let's find the prime factorization of 2, 4, and 5:
- 2 = 2¹
- 4 = 2²
- 5 = 5¹
The prime factors involved are 2 and 5. Taking the highest power of each prime factor:
- Highest power of 2: 2² = 4
- Highest power of 5: 5¹ = 5
Multiplying these highest powers together: 4 * 5 = 20
Therefore, the LCM of 2, 4, and 5 is 20.
Advantages: Efficient and systematic, works well for larger numbers and multiple integers.
Disadvantages: Requires knowledge of prime factorization.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the GCD (Greatest Common Divisor) of two or more numbers. The formula connecting LCM and GCD is:
(LCM(a, b, c...) * GCD(a, b, c...) = a * b * c...)
First, we need to find the GCD of 2, 4, and 5. The GCD is the largest number that divides all the given numbers without leaving a remainder. In this case, the GCD of 2, 4, and 5 is 1 (because 1 is the only common divisor).
Let's denote:
- a = 2
- b = 4
- c = 5
Using the formula:
LCM(2, 4, 5) * GCD(2, 4, 5) = 2 * 4 * 5
LCM(2, 4, 5) * 1 = 40
Therefore, LCM(2, 4, 5) = 20
Advantages: Provides a concise and efficient method, especially when dealing with larger numbers where prime factorization can become complex.
Disadvantages: Requires understanding of both LCM and GCD concepts and their relationship.
Applications of LCM
The concept of LCM finds applications in various fields:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator. This simplifies the process significantly.
2. Scheduling Problems
Imagine two buses depart from the same stop, one every 2 hours and the other every 4 hours. To find when both buses will depart simultaneously again, you need to find the LCM of 2 and 4, which is 4. Therefore, both buses will depart at the same time again after 4 hours.
3. Music Theory
LCM plays a role in understanding musical rhythms and creating harmonies. Different musical notes have different durations, and LCM helps to determine when those notes will align again.
4. Gear Ratios
In mechanical systems, gear ratios involve the LCM to determine when different gears will complete a full rotation cycle simultaneously.
5. Project Management
In complex projects with multiple tasks that have different durations, the LCM can help in determining the project completion time or synchronization points.
Conclusion
Calculating the least common multiple (LCM) is a fundamental mathematical operation with widespread applications. We have explored three different methods – listing multiples, prime factorization, and the GCD method – each offering unique advantages and disadvantages. The choice of the most suitable method depends on the specific context and the numbers involved. Understanding LCM is essential for anyone working with fractions, scheduling, music theory, or various other areas where synchronization and cyclical events are important. The LCM of 2, 4, and 5, as we've thoroughly demonstrated, is 20, a result achievable through each of the explained methods. Mastering this concept enhances problem-solving skills and broadens mathematical understanding.
Latest Posts
Latest Posts
-
How Much Is 40 000 United Miles Worth
May 11, 2025
-
Which Unit Is An Acceptable Way To Measure Urinary Output
May 11, 2025
-
1 1 2 As A Improper Fraction
May 11, 2025
-
Find The Area Of The Given Figure
May 11, 2025
-
How Many Ounces Are In 2 And 1 2 Cups
May 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 4 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.