Lcm Of 2 6 And 11
Treneri
May 10, 2025 · 5 min read
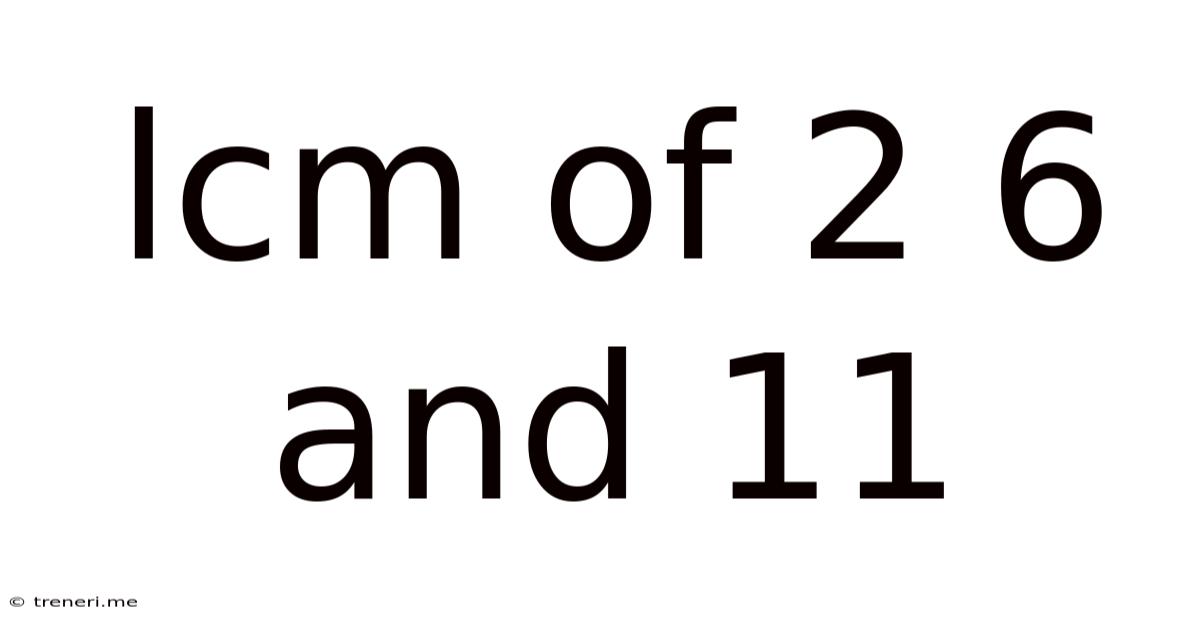
Table of Contents
Finding the Least Common Multiple (LCM) of 2, 6, and 11: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in number theory with wide-ranging applications in mathematics, computer science, and various other fields. This article delves into the process of calculating the LCM of 2, 6, and 11, exploring different methods and providing a thorough understanding of the underlying principles. We'll also touch upon the broader significance of LCMs and their practical uses.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific LCM of 2, 6, and 11, let's establish a solid understanding of what an LCM represents. The LCM of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. This concept is crucial in various mathematical operations and problem-solving scenarios.
For example, consider two numbers, 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20... and the multiples of 6 are 6, 12, 18, 24... The common multiples are 12, 24, 36... The smallest of these common multiples is 12, hence the LCM(4, 6) = 12.
Methods for Calculating the LCM
Several methods exist for calculating the LCM of a set of numbers. We'll explore the most common and efficient approaches, focusing on their application to finding the LCM of 2, 6, and 11.
1. Prime Factorization Method
This method is arguably the most robust and widely applicable technique for determining the LCM. It involves breaking down each number into its prime factors. The prime factors are the fundamental building blocks of a number, representing its indivisible components.
-
Step 1: Prime Factorization:
- 2 = 2
- 6 = 2 × 3
- 11 = 11 (11 is a prime number)
-
Step 2: Identifying the Highest Power of Each Prime Factor: We examine the prime factorization of each number and identify the highest power of each distinct prime factor present. In this case:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 11 is 11¹ = 11
-
Step 3: Calculating the LCM: Multiply the highest powers of all the distinct prime factors together to obtain the LCM.
LCM(2, 6, 11) = 2 × 3 × 11 = 66
Therefore, the least common multiple of 2, 6, and 11 is 66.
2. Listing Multiples Method
This method is straightforward for smaller numbers but becomes less efficient as the numbers increase in size. It involves listing the multiples of each number until a common multiple is found.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 66, 68...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 66, 72...
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77...
The smallest common multiple among these lists is 66. Therefore, LCM(2, 6, 11) = 66. This method, while simple conceptually, can become quite tedious for larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. Using the formula:
LCM(a, b, c) = (|a × b × c|) / GCD(a, b, c)
However, this formula is not directly applicable to finding the LCM of three or more numbers without some modification, requiring iterative application. This means you'd find the GCD of two numbers, then find the GCD of the result and the third number. For this reason the prime factorization method is more efficient for three or more numbers.
Applications of LCM
The LCM has numerous applications across various disciplines:
-
Scheduling and Time Management: Determining when events will occur simultaneously (e.g., finding the next time two buses arrive at a stop at the same time).
-
Fractions: Finding the least common denominator when adding or subtracting fractions. This is crucial for simplifying fraction arithmetic.
-
Modular Arithmetic: LCM is essential in solving congruences, a crucial aspect of number theory with significant uses in cryptography and computer science.
-
Music Theory: Determining the harmonic intervals between different musical notes relies on understanding common multiples.
-
Engineering: In certain engineering calculations involving periodic phenomena or repeating processes, finding the LCM is necessary for coordination and optimization.
Beyond the Basics: LCM of Larger Numbers
The methods outlined above are applicable to any set of integers. For larger numbers, the prime factorization method remains the most computationally efficient. However, factoring large numbers into their prime components can become computationally intensive. Advanced algorithms and software are used to handle such cases.
The concept of LCM extends to more than three numbers. The principles remain the same; we simply need to extend the prime factorization method to include all the numbers in the set.
Conclusion
Calculating the LCM of 2, 6, and 11, whether using prime factorization, listing multiples, or a more sophisticated approach, demonstrates a fundamental concept in mathematics with significant practical applications. Understanding the LCM is crucial for various mathematical operations and problem-solving across various fields. Choosing the most efficient method depends on the numbers involved, with the prime factorization method offering the greatest versatility and efficiency for larger or more complex sets of numbers. Mastering LCM calculations empowers you to tackle numerous problems involving cycles, timing, and fractions with greater precision and efficiency. Remember, the underlying concept remains constant regardless of the method employed.
Latest Posts
Latest Posts
-
What Is A Good Tanning Uv
May 10, 2025
-
Cuanto Es 8 Onzas En Litros
May 10, 2025
-
Round 66 To The Nearest Ten
May 10, 2025
-
Cuanto Falta Para El 18 De Noviembre
May 10, 2025
-
If A Triangle Has A Height Of 12 Inches
May 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 6 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.