Lcm Of 2 8 And 12
Treneri
May 10, 2025 · 5 min read
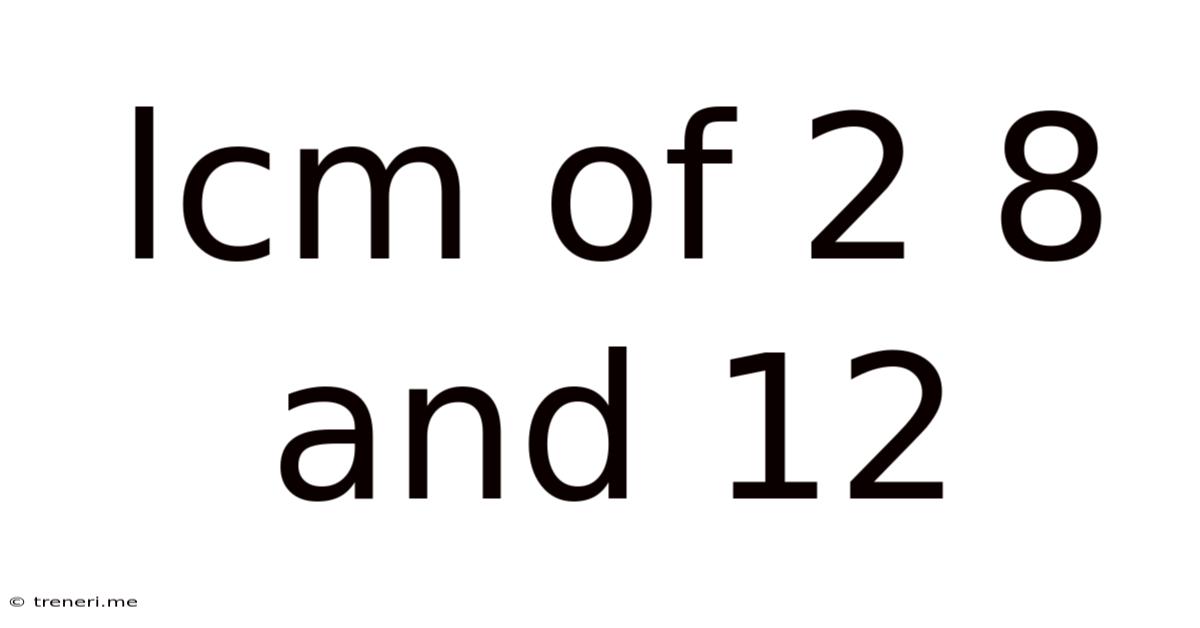
Table of Contents
Finding the LCM of 2, 8, and 12: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. Understanding LCM is crucial for various applications, including simplifying fractions, solving problems involving cycles or periodic events, and working with rational numbers. This comprehensive guide will walk you through the process of finding the LCM of 2, 8, and 12, exploring different methods and providing a deeper understanding of the underlying principles.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
Distinguishing LCM from Greatest Common Divisor (GCD)
It's important to differentiate LCM from the greatest common divisor (GCD). The GCD is the largest positive integer that divides all the given integers without leaving a remainder. While related, LCM and GCD are distinct concepts. For instance, the GCD of 12 and 18 is 6, whereas the LCM is 36.
Methods for Finding the LCM of 2, 8, and 12
Several methods can be used to find the LCM of 2, 8, and 12. We'll explore the most common and efficient approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24...
- Multiples of 8: 8, 16, 24, 32, 40...
- Multiples of 12: 12, 24, 36, 48...
Observing the lists, we see that the smallest multiple common to 2, 8, and 12 is 24. Therefore, the LCM(2, 8, 12) = 24.
This method is simple but becomes less practical with larger numbers or a greater number of integers.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a more structured approach. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 2: 2¹
- Prime factorization of 8: 2³
- Prime factorization of 12: 2² * 3¹
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
Now, multiply these highest powers together: 8 * 3 = 24. Therefore, LCM(2, 8, 12) = 24.
This method is generally preferred for its efficiency and systematic approach, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between LCM and GCD. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This can be extended to more than two numbers, but the process becomes slightly more complex. We'll demonstrate with two numbers at a time:
First, find the GCD of 2 and 8 using the Euclidean algorithm or prime factorization. The GCD(2, 8) = 2.
Then, using the formula: LCM(a, b) = (a * b) / GCD(a, b), we get LCM(2, 8) = (2 * 8) / 2 = 8.
Now, we find the LCM of 8 and 12. The GCD(8, 12) = 4. Therefore, LCM(8, 12) = (8 * 12) / 4 = 24.
Thus, LCM(2, 8, 12) = 24.
While this method works, it can be more computationally intensive than the prime factorization method for larger numbers.
Applications of Finding the LCM
The LCM has numerous applications across various fields:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator. This simplifies the process and allows for accurate calculations. For example, to add 1/2 + 1/8 + 1/12, you'd find the LCM(2, 8, 12) = 24, then convert each fraction to have a denominator of 24 before adding them.
2. Cyclic Events
LCM is extensively used to solve problems involving events that repeat cyclically. For example, imagine three buses that arrive at a station every 2, 8, and 12 minutes, respectively. The LCM(2, 8, 12) = 24 indicates that all three buses will arrive at the station simultaneously every 24 minutes.
3. Gears and Rotating Objects
In engineering and mechanics, LCM is used to determine the synchronization of gears or other rotating objects. The LCM of the rotation speeds dictates when the objects will be in the same relative position.
4. Scheduling and Planning
LCM is helpful in scheduling tasks or events that occur at regular intervals. It helps to determine the time when all events coincide.
5. Number Theory and Abstract Algebra
LCM plays a significant role in various aspects of number theory, such as modular arithmetic and the study of divisibility. It also has applications in abstract algebra, specifically in ring theory and ideal theory.
Beyond the Basics: Extending the LCM Concept
While we focused on finding the LCM of three integers, the principles extend to any number of integers. The prime factorization method remains a powerful tool for finding the LCM of larger sets of numbers. Software and online calculators can also assist with complex LCM calculations.
Furthermore, the concept of LCM can be extended to other mathematical structures beyond integers, such as polynomials. Finding the LCM of polynomials involves factoring them into irreducible polynomials and selecting the highest power of each irreducible factor, similar to the method used with integers.
Conclusion: Mastering LCM for Mathematical Proficiency
Understanding and applying the LCM is a crucial skill in mathematics. This guide has provided a comprehensive explanation of the concept, various methods for calculation, and practical applications across several fields. Whether you're a student tackling arithmetic problems or a professional working with complex systems, mastering the LCM enhances your mathematical proficiency and problem-solving abilities. Remember to choose the method best suited to the specific problem and the numbers involved for optimal efficiency. By grasping these fundamental concepts, you'll be well-equipped to tackle a wider range of mathematical challenges.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 2 And 8
May 10, 2025
-
What Is 15 Percent Of 30000
May 10, 2025
-
Cuanto Son 85 Kilos En Libras
May 10, 2025
-
Common Multiples Of 5 And 2
May 10, 2025
-
3 Cloves Of Minced Garlic In Tablespoons
May 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.