Lcm Of 3 5 And 10
Treneri
May 14, 2025 · 5 min read
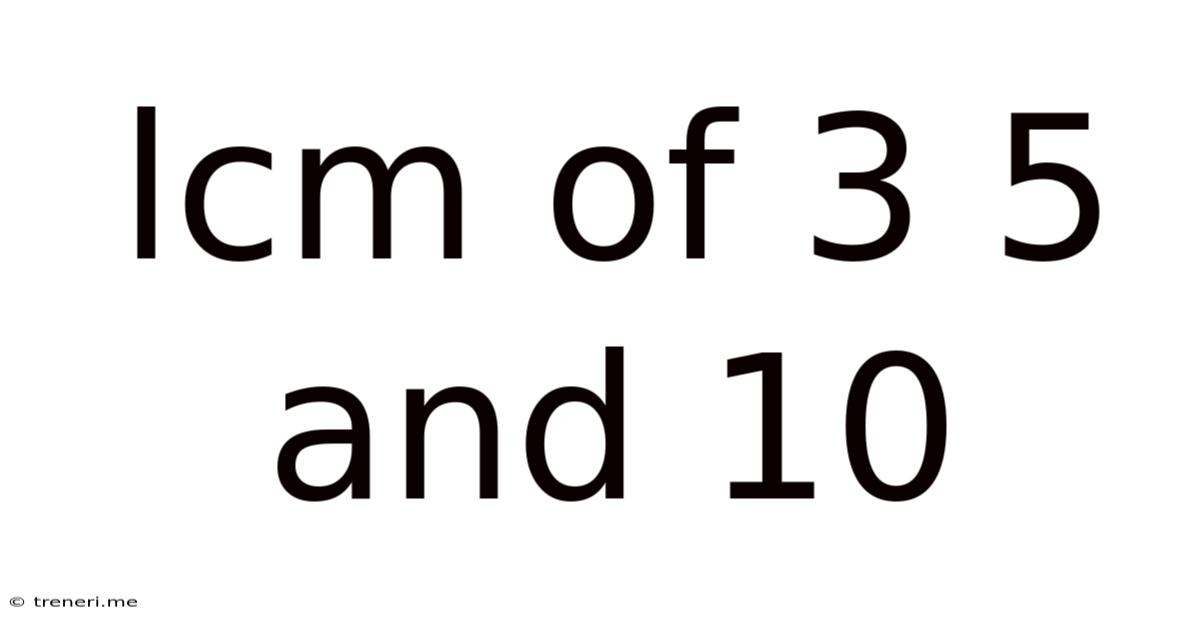
Table of Contents
Finding the LCM of 3, 5, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding LCMs is crucial for various applications, from simplifying fractions to solving problems involving cycles and periodic events. This article delves into the process of finding the LCM of 3, 5, and 10, exploring multiple methods and providing a deeper understanding of the underlying principles. We'll also examine the broader context of LCMs and their significance.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer divisible by both 2 and 3. Finding the LCM is a common task in many mathematical operations and real-world applications.
Why is finding the LCM important?
The LCM has numerous practical applications:
-
Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions requires calculating the LCM of the denominators. This simplifies the process and ensures accurate results.
-
Scheduling and Cycles: LCMs are essential for solving problems involving repeating cycles or events. For instance, if two machines have different operating cycles, the LCM helps determine when they will both be at the beginning of their cycles simultaneously.
-
Modular Arithmetic: LCMs play a crucial role in modular arithmetic, which has applications in cryptography, computer science, and other fields.
-
Music Theory: In music, LCMs help determine the least common denominator of time signatures, which is essential for creating harmonic and rhythmic structures.
Methods for Finding the LCM of 3, 5, and 10
There are several efficient methods for determining the LCM of a set of numbers. Let's explore the most common techniques applied to find the LCM of 3, 5, and 10:
1. Listing Multiples Method
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 10: 10, 20, 30...
By inspecting the lists, we observe that the smallest common multiple is 30. Therefore, the LCM(3, 5, 10) = 30.
This method is simple but can become cumbersome for larger numbers or a larger set of numbers.
2. Prime Factorization Method
This method is more efficient, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 3: 3
- Prime factorization of 5: 5
- Prime factorization of 10: 2 x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
Multiplying these highest powers together, we get: 2 x 3 x 5 = 30. Thus, the LCM(3, 5, 10) = 30.
This method is more systematic and works well even with larger numbers, making it a preferred approach for more complex LCM calculations.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of a set of numbers are related through the following formula:
LCM(a, b) * GCD(a, b) = a * b
This relationship holds for two numbers. To extend it to three or more numbers, we can find the LCM iteratively. First, find the LCM of two numbers, then find the LCM of that result and the next number, and so on. For our example, let's use the GCD method iteratively.
First, let's find the GCD of 3 and 5 using the Euclidean algorithm:
- 5 = 1 * 3 + 2
- 3 = 1 * 2 + 1
- 2 = 2 * 1 + 0
The GCD(3, 5) = 1.
Now, using the formula:
LCM(3, 5) * GCD(3, 5) = 3 * 5 LCM(3, 5) * 1 = 15 LCM(3, 5) = 15
Next, we find the LCM of 15 and 10:
First find the GCD(15,10):
- 15 = 1 * 10 + 5
- 10 = 2 * 5 + 0
GCD(15,10) = 5
Now, using the formula again:
LCM(15, 10) * GCD(15, 10) = 15 * 10 LCM(15, 10) * 5 = 150 LCM(15, 10) = 30
Therefore, the LCM(3, 5, 10) = 30.
Understanding the Relationship Between LCM and GCD
The LCM and GCD are intrinsically linked. For any two integers a and b, the product of their LCM and GCD is equal to the product of the two integers:
LCM(a, b) * GCD(a, b) = a * b
This property is useful because it allows us to calculate one if we know the other. For example, if we know the GCD of two numbers, we can easily compute their LCM using this formula. This relationship extends to more than two numbers, but the calculation becomes more complex.
Applications of LCM in Real-World Scenarios
Beyond the theoretical realm, LCMs find practical applications in various situations:
-
Synchronization of Events: Imagine two buses departing from the same station at different intervals. The LCM of their departure intervals determines when they will depart simultaneously again.
-
Task Scheduling: In project management, if different tasks have different completion cycles, the LCM can be used to determine the next time all tasks will be completed simultaneously.
-
Gear Ratios: In mechanics, gear ratios often involve LCMs to determine the optimal gear combinations for smooth operation and efficiency.
-
Periodic Phenomena: In physics and engineering, many phenomena are periodic, like wave patterns or machine cycles. LCMs help in analyzing the synchronization and overlap of such phenomena.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a valuable skill with numerous applications across different fields. This article has provided a detailed explanation of different methods to calculate the LCM, focusing on the example of 3, 5, and 10. Mastering these techniques enables you to tackle more complex problems involving LCM calculations efficiently. Remember that choosing the right method depends on the numbers involved; the prime factorization method generally provides a more efficient approach for larger numbers. Understanding the relationship between the LCM and GCD provides additional tools for solving these mathematical problems. The ability to confidently calculate LCMs opens doors to a deeper understanding of mathematical concepts and their practical implications.
Latest Posts
Latest Posts
-
Solve For X In A Triangle
May 14, 2025
-
How Much Meat For 200 People
May 14, 2025
-
10 454 Sqft Lot Size In Acres
May 14, 2025
-
16 Rounded To The Nearest Tenth
May 14, 2025
-
How Much Is 450 Grams In Ounces
May 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.