Lcm Of 3 7 And 10
Treneri
May 11, 2025 · 5 min read
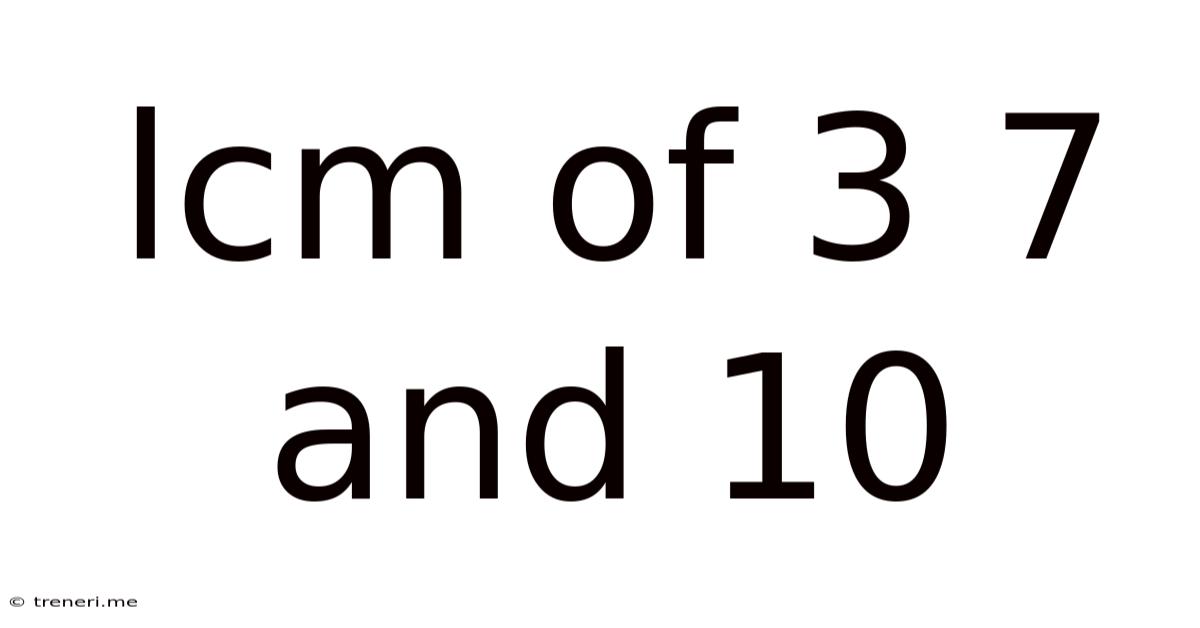
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 7, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics with widespread applications, from simple fraction operations to complex scheduling problems. This comprehensive guide will delve into the process of calculating the LCM of 3, 7, and 10, exploring various methods and providing a solid understanding of the underlying principles. We'll also explore the broader significance of LCMs and their practical applications.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific calculation for 3, 7, and 10, let's solidify our understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
For instance, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
This concept extends to more than two numbers. We'll now apply this understanding to find the LCM of 3, 7, and 10.
Method 1: Listing Multiples
This is a straightforward method, especially when dealing with smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 70, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, ...
By examining the lists, we can see that the smallest number present in all three lists is 210. Therefore, the LCM of 3, 7, and 10 using this method is 210. However, this method becomes less practical with larger numbers.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime Factorization of 3: 3 (3 is itself a prime number)
- Prime Factorization of 7: 7 (7 is itself a prime number)
- Prime Factorization of 10: 2 x 5
Now, we construct the LCM by taking the highest power of each prime factor present in the factorizations:
- We have 2, 3, 5, and 7 as prime factors.
- The highest power of 2 is 2<sup>1</sup> = 2.
- The highest power of 3 is 3<sup>1</sup> = 3.
- The highest power of 5 is 5<sup>1</sup> = 5.
- The highest power of 7 is 7<sup>1</sup> = 7.
Multiply these highest powers together: 2 x 3 x 5 x 7 = 210.
Therefore, the LCM of 3, 7, and 10 using prime factorization is 210. This method is significantly more efficient for larger numbers where listing multiples becomes cumbersome.
Method 3: Using the Formula (for Two Numbers)
While there isn't a direct formula for finding the LCM of three or more numbers at once, we can use the formula for two numbers iteratively. The formula for the LCM of two numbers, a and b, is:
LCM(a, b) = (a * b) / GCD(a, b)
Where GCD(a, b) is the greatest common divisor of a and b.
Let's apply this iteratively:
-
Find the LCM of 3 and 7:
- GCD(3, 7) = 1 (3 and 7 have no common factors other than 1)
- LCM(3, 7) = (3 * 7) / 1 = 21
-
Find the LCM of 21 and 10:
- GCD(21, 10) = 1 (21 and 10 have no common factors other than 1)
- LCM(21, 10) = (21 * 10) / 1 = 210
Therefore, the LCM of 3, 7, and 10 using this iterative method is 210.
Applications of LCM in Real Life
The concept of LCM finds practical applications in various scenarios:
-
Scheduling: Imagine two buses departing from the same station, one every 3 hours and the other every 7 hours. The LCM helps determine when both buses will depart at the same time again. In this case, the LCM(3, 7) = 21, meaning they'll depart simultaneously every 21 hours.
-
Fraction Operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator.
-
Project Management: In projects with multiple tasks having different completion times, the LCM can help in scheduling tasks for efficient resource utilization and avoiding conflicts.
-
Music: LCM helps in understanding musical rhythms and harmonies where different musical phrases repeat at varying intervals.
-
Gear Ratios: In mechanical engineering, determining gear ratios often involves LCM calculations to ensure smooth operation.
Conclusion: Mastering LCM Calculations
This guide has provided a thorough understanding of how to calculate the LCM of 3, 7, and 10 using various methods. While the listing method is suitable for smaller numbers, prime factorization and the iterative GCD/LCM formula prove more efficient for larger numbers and more complex scenarios. Understanding LCM is crucial for solving numerous mathematical problems and applying mathematical concepts in real-world situations across diverse fields. Remember, the key takeaway is that the LCM of 3, 7, and 10 is definitively 210, regardless of the chosen method. Practice these methods to solidify your understanding and increase your problem-solving capabilities. The ability to efficiently find LCMs is a valuable skill that will serve you well in various mathematical and practical contexts.
Latest Posts
Latest Posts
-
Creatinine From Mmol L To Mg Dl
May 11, 2025
-
How Many Days From August 1 To December 31 2024
May 11, 2025
-
35 Kilometers Is How Many Miles
May 11, 2025
-
How Many Cbm In 40ft Container
May 11, 2025
-
How Do You Find The Exact Area Of A Circle
May 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 7 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.