Lcm Of 6 4 And 10
Treneri
May 15, 2025 · 4 min read
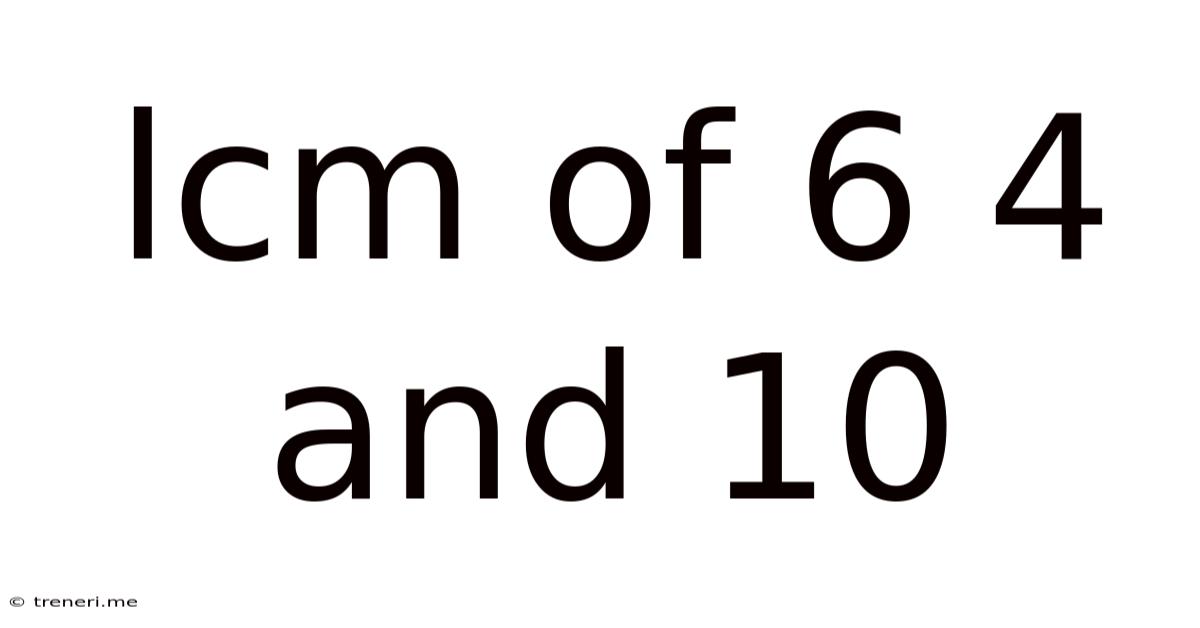
Table of Contents
Finding the LCM of 6, 4, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications, from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will delve into the process of determining the LCM of 6, 4, and 10, exploring various methods and offering a deeper understanding of the underlying principles. We'll cover everything from basic definitions to advanced techniques, ensuring a thorough grasp of this essential mathematical skill.
Understanding Least Common Multiple (LCM)
Before tackling the LCM of 6, 4, and 10, let's solidify our understanding of the concept itself. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This contrasts with the greatest common divisor (GCD), which is the largest number that divides all the given numbers without a remainder.
Key takeaway: The LCM represents the smallest shared multiple among a set of numbers.
Method 1: Listing Multiples
This method, while simple for smaller numbers, involves listing the multiples of each number until a common multiple is found.
Steps:
- List multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- List multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, ...
- List multiples of 10: 10, 20, 30, 40, 50, 60, ...
By comparing the lists, we can identify the smallest number that appears in all three lists: 60.
Therefore, the LCM of 6, 4, and 10 is 60.
This method is straightforward but becomes less efficient with larger numbers.
Method 2: Prime Factorization
This is a more efficient and reliable method, especially for larger numbers. It involves breaking down each number into its prime factors.
Steps:
-
Find the prime factorization of each number:
- 6 = 2 x 3
- 4 = 2 x 2 = 2²
- 10 = 2 x 5
-
Identify the highest power of each prime factor present:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers together: 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, the LCM of 6, 4, and 10 is 60.
This method is more systematic and works effectively for numbers of any size.
Method 3: Using the GCD (Greatest Common Divisor)
The LCM and GCD are closely related. We can utilize the GCD to calculate the LCM using the following formula:
LCM(a, b) x GCD(a, b) = a x b
This formula applies to two numbers initially. To extend this to three or more numbers, we can calculate the LCM in stages.
Steps:
-
Find the GCD of 6 and 4 using the Euclidean algorithm or prime factorization:
- Prime factorization: 6 = 2 x 3; 4 = 2 x 2. The GCD(6, 4) = 2.
-
Calculate the LCM of 6 and 4 using the formula:
- LCM(6, 4) x GCD(6, 4) = 6 x 4
- LCM(6, 4) x 2 = 24
- LCM(6, 4) = 12
-
Find the GCD of 12 (the LCM of 6 and 4) and 10:
- Prime factorization: 12 = 2² x 3; 10 = 2 x 5. The GCD(12, 10) = 2.
-
Calculate the LCM of 12 and 10 using the formula:
- LCM(12, 10) x GCD(12, 10) = 12 x 10
- LCM(12, 10) x 2 = 120
- LCM(12, 10) = 60
Therefore, the LCM of 6, 4, and 10 is 60. This method demonstrates the interconnectedness of LCM and GCD.
Applications of LCM
Understanding LCM has far-reaching applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Scheduling Problems: Determining when events with different periodicities will coincide (e.g., buses arriving at a stop).
-
Music Theory: Calculating the least common multiple of note durations to determine when rhythms will align.
-
Engineering and Construction: Coordinating tasks with different cycle times.
-
Computer Science: Optimizing algorithms and data structures.
Advanced Techniques and Considerations
For a larger set of numbers or extremely large numbers, more advanced algorithms are employed. These often involve sophisticated techniques from number theory, including:
-
Euclidean Algorithm: A highly efficient method for finding the GCD of two numbers, which, as demonstrated earlier, can then be used to compute the LCM.
-
Least Common Multiple Algorithm (LCMA): This is an algorithm specifically designed to efficiently compute the LCM of multiple numbers.
Conclusion
Finding the LCM of 6, 4, and 10, as demonstrated through multiple methods, highlights the importance of understanding this fundamental mathematical concept. While simple methods suffice for smaller numbers, the prime factorization method provides a robust and efficient approach for numbers of any size. Understanding the relationships between LCM and GCD, along with exploring the various applications, solidifies the practical value of this crucial mathematical tool. The ability to calculate LCM efficiently contributes significantly to problem-solving across numerous disciplines, making it a valuable skill to master. From simplifying everyday tasks to tackling advanced mathematical and scientific challenges, the concept of LCM continues to demonstrate its importance in both theoretical and practical realms.
Latest Posts
Latest Posts
-
88 83 Is What Percent Of 21
May 15, 2025
-
Cuantas Semanas Tiene Un Ano De 365 Dias
May 15, 2025
-
How Many Ounce In A Kilogram
May 15, 2025
-
How Many Cubic Feet Is 55 Quarts Of Potting Soil
May 15, 2025
-
What Is The Gcf For 18 And 32
May 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 4 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.