Lcm Of 7 4 And 2
Treneri
May 15, 2025 · 4 min read
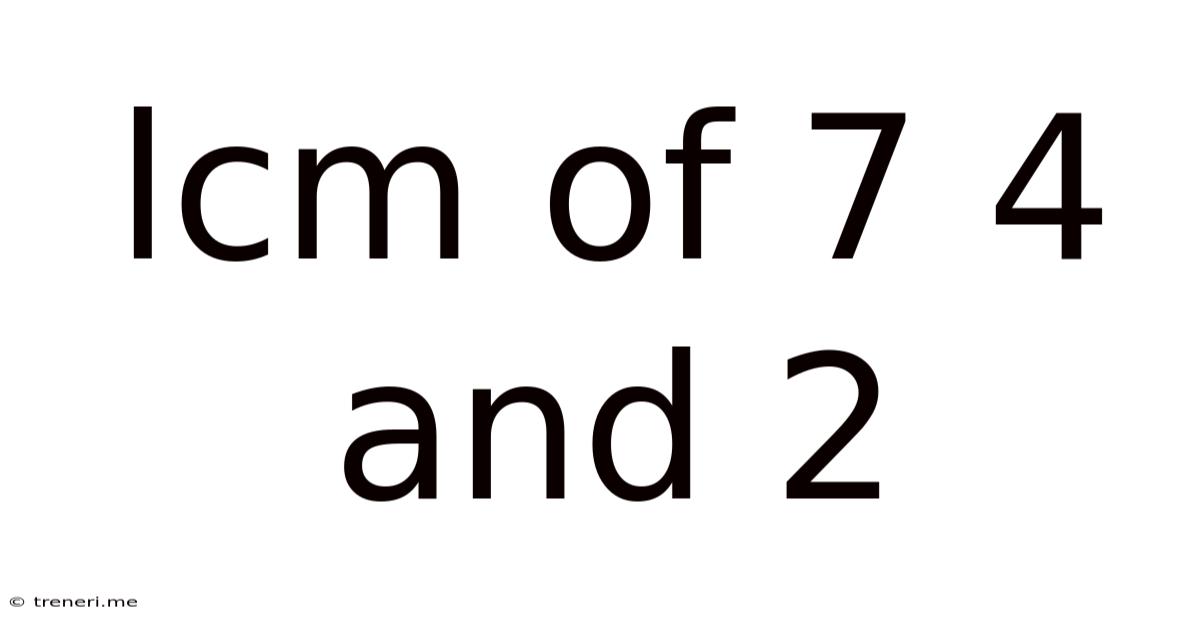
Table of Contents
Finding the Least Common Multiple (LCM) of 7, 4, and 2: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with widespread applications in various fields, from scheduling problems to music theory. This article provides a thorough exploration of how to find the LCM of 7, 4, and 2, detailing different methods and explaining the underlying principles. We will delve into the significance of LCM and its practical applications, offering a comprehensive understanding for both beginners and those seeking a refresher.
Understanding Least Common Multiple (LCM)
Before we tackle the specific calculation for the LCM of 7, 4, and 2, let's establish a solid understanding of what LCM actually means. The LCM of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly without leaving a remainder.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by each of the given integers.
- Smallest: It's the smallest positive integer that satisfies the divisibility condition.
Methods for Calculating LCM
Several methods exist for determining the LCM, each with its own advantages and disadvantages. We'll explore the most common approaches, applying them to find the LCM of 7, 4, and 2.
Method 1: Listing Multiples
This method is straightforward but can become tedious for larger numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, ...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, ...
By comparing the lists, we observe that the smallest common multiple of 7, 4, and 2 is 28.
Method 2: Prime Factorization
This method is generally more efficient, especially when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
-
Prime Factorization:
- 7 = 7 (7 is a prime number)
- 4 = 2²
- 2 = 2
-
Constructing the LCM: We take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2².
- The highest power of 7 is 7.
-
Calculating the LCM: Multiply the highest powers together: 2² * 7 = 4 * 7 = 28
Therefore, the LCM of 7, 4, and 2 is 28.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. The product of the LCM and GCD of two or more numbers is equal to the product of the numbers themselves. This relationship can be used to calculate the LCM if the GCD is known.
-
Finding the GCD: The GCD of 7, 4, and 2 is 1 (since they share no common factors other than 1).
-
Using the Formula: Let's consider the numbers a, b, and c. The relationship between LCM and GCD is:
LCM(a, b, c) * GCD(a, b, c) = a * b * c
In our case:
LCM(7, 4, 2) * GCD(7, 4, 2) = 7 * 4 * 2
LCM(7, 4, 2) * 1 = 56
Therefore, LCM(7, 4, 2) = 28
Applications of LCM
The LCM finds applications in diverse fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if three buses depart from a station at intervals of 7, 4, and 2 hours, respectively, the LCM (28 hours) indicates when they will all depart at the same time.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Music Theory: Calculating the least common multiple of note durations to find when rhythms synchronize.
-
Gear Ratios: In mechanical engineering, the LCM helps determine the synchronization of rotating gears with different numbers of teeth.
Choosing the Right Method
The best method for finding the LCM depends on the context and the numbers involved.
- For small numbers, listing multiples is straightforward.
- For larger numbers, prime factorization is generally more efficient.
- The GCD method is useful when the GCD is already known or easily calculated.
Conclusion
Finding the LCM of 7, 4, and 2, as demonstrated through various methods, solidifies the understanding of this fundamental mathematical concept. The LCM’s practical applications extend far beyond the classroom, demonstrating its importance in various real-world scenarios. This comprehensive guide serves as a valuable resource for anyone seeking to master the calculation and application of the least common multiple. Understanding LCM is not merely an academic exercise; it's a crucial tool for problem-solving across diverse disciplines. By grasping the different methods and their respective strengths, one can effectively tackle LCM calculations and appreciate its significance in numerous fields. The versatility and practicality of this mathematical concept underscore its importance in both theoretical and applied contexts.
Latest Posts
Latest Posts
-
88 83 Is What Percent Of 21
May 15, 2025
-
Cuantas Semanas Tiene Un Ano De 365 Dias
May 15, 2025
-
How Many Ounce In A Kilogram
May 15, 2025
-
How Many Cubic Feet Is 55 Quarts Of Potting Soil
May 15, 2025
-
What Is The Gcf For 18 And 32
May 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 4 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.