Lcm Of 7 5 And 2
Treneri
May 11, 2025 · 5 min read
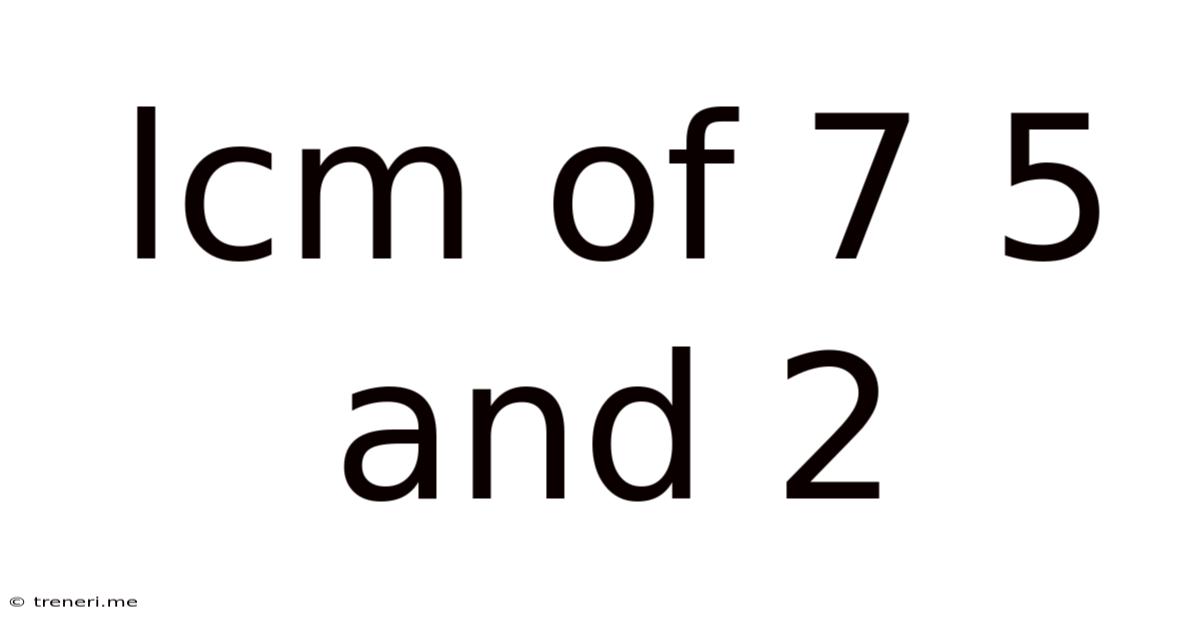
Table of Contents
Finding the LCM of 7, 5, and 2: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in various fields like scheduling, music theory, and even computer programming. This article will delve into the process of calculating the LCM of 7, 5, and 2, providing a thorough understanding of the underlying principles and multiple methods for achieving the solution. We’ll explore the concept of LCM, its significance, and diverse approaches to calculating it, including manual methods and utilizing prime factorization.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it’s the smallest number that contains all the given numbers as its factors. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer that is divisible by both 2 and 3.
This concept has practical applications in various areas:
- Scheduling: Determining the time when two or more events will occur simultaneously, such as scheduling meetings or bus routes.
- Music: Finding the lowest common denominator in musical rhythms, aiding in composing harmonious melodies.
- Fractions: Finding the least common denominator when adding or subtracting fractions.
- Computer Science: Solving problems related to timing, synchronization, and data processing.
Methods to Find the LCM of 7, 5, and 2
Several methods can be employed to calculate the LCM of 7, 5, and 2. Let's explore the most common ones:
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. While straightforward for smaller numbers, it can become cumbersome for larger numbers.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77…
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70…
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70…
Observing the lists, we find that 70 is the smallest number that appears in all three lists. Therefore, the LCM of 7, 5, and 2 is 70.
2. Prime Factorization Method
This method involves finding the prime factors of each number and then constructing the LCM using the highest powers of each prime factor. This is a more efficient method, especially when dealing with larger numbers.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 2: 2 (2 is a prime number)
Since 7, 5, and 2 are all prime numbers and have no common factors, the LCM is simply the product of these three numbers.
LCM(7, 5, 2) = 7 × 5 × 2 = 70
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are related through the following formula:
LCM(a, b, c) = (a × b × c) / GCD(a, b, c)
However, this formula is most effective when dealing with numbers that share common factors. Since 7, 5, and 2 are all prime numbers and don't share any common factors other than 1, their GCD is 1. Applying this method:
LCM(7, 5, 2) = (7 × 5 × 2) / GCD(7, 5, 2) = 70 / 1 = 70
Why is understanding LCM important?
The concept of LCM is surprisingly versatile and its understanding extends beyond simple mathematical calculations. Let's explore some real-world examples:
1. Scheduling and Synchronization:
Imagine you have three different machines in a factory, each operating on a specific cycle:
- Machine A completes a cycle every 7 minutes.
- Machine B completes a cycle every 5 minutes.
- Machine C completes a cycle every 2 minutes.
To determine when all three machines will complete a cycle simultaneously, you need to find the LCM of 7, 5, and 2. The LCM, 70, tells us that all three machines will complete a cycle at the same time after 70 minutes.
2. Music Theory:
In music, rhythms are often represented as fractions of a beat. Finding the LCM is essential to determine the shortest duration that encompasses all the rhythms in a musical phrase, ensuring a seamless and harmonious flow.
3. Fraction Addition and Subtraction:
When adding or subtracting fractions with different denominators, you need to find the least common denominator (LCD), which is the LCM of the denominators. This step is critical for accurate calculations. For example, adding 1/7, 1/5, and 1/2 requires finding the LCM of 7, 5, and 2 (which is 70) to create a common denominator.
4. Computer Programming:
In programming tasks involving timing and synchronization, the LCM is used to determine the frequency of specific events or to align different processes. This is frequently used in applications dealing with real-time systems and parallel processing.
Advanced LCM Concepts and Considerations
While we've focused on the LCM of 7, 5, and 2, the concept extends to more complex scenarios:
- LCM of more than three numbers: The same principles apply when calculating the LCM of four or more numbers. You can employ the prime factorization method or iterative approaches.
- LCM of non-integers: While the focus is typically on integers, the concept of LCM can be extended to other number systems like rational numbers, with appropriate adaptations to the methods.
- Algorithms for efficient LCM calculation: For extremely large numbers, specialized algorithms are developed to efficiently compute the LCM without requiring extensive computational resources. These often leverage advanced mathematical properties and data structures.
Conclusion: Mastering the LCM
Understanding and calculating the least common multiple is a fundamental skill with wide-ranging applications. This article provided various methods, from the straightforward listing of multiples to the more efficient prime factorization approach. By understanding these methods and their underlying principles, you gain a crucial tool for solving problems across diverse fields, including scheduling, music theory, and programming. Remember, mastering the LCM is not just about getting the right answer but also about grasping the underlying mathematical concepts and their practical significance. The LCM of 7, 5, and 2, determined to be 70, serves as a clear example of how this seemingly simple concept plays a vital role in more complex applications. Keep practicing, and you'll find that the ability to calculate LCM becomes a valuable asset in your mathematical arsenal.
Latest Posts
Latest Posts
-
How Do You Find The Exact Area Of A Circle
May 11, 2025
-
What Is The Volume Of The Cone Below Apex
May 11, 2025
-
How Much Longer Till 6 Am
May 11, 2025
-
15 Is What Percent Of 120
May 11, 2025
-
How Many Days Is 5 Month
May 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 5 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.