Lcm Of 8 10 And 15
Treneri
May 15, 2025 · 5 min read
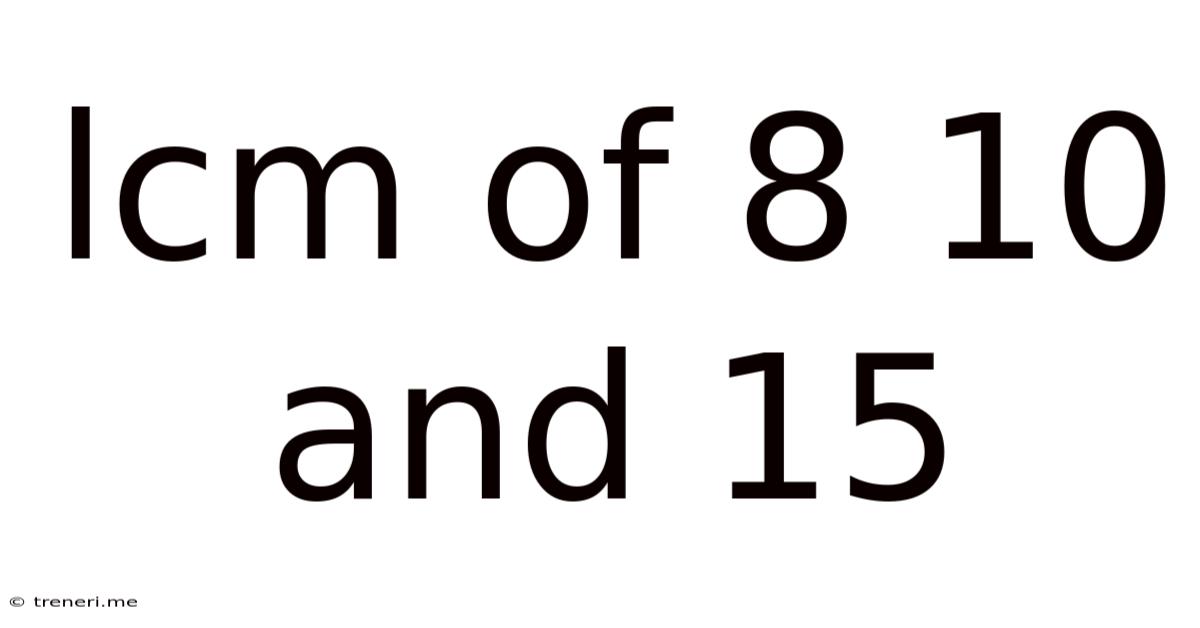
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 10, and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in number theory and algebra. Understanding how to calculate the LCM is essential for solving various problems, from simplifying fractions to scheduling events. This comprehensive guide will delve into the process of finding the LCM of 8, 10, and 15, exploring multiple methods and providing a solid foundation for understanding this key mathematical concept. We’ll also explore the practical applications of LCM calculations.
Understanding Least Common Multiples
Before diving into the calculation, let's clarify what the LCM represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. In simpler terms, it's the smallest number that all the numbers you're considering can divide into evenly.
For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16...
- Multiples of 3: 3, 6, 9, 12, 15, 18...
The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Calculating the LCM of 8, 10, and 15
There are several effective methods for calculating the LCM, each with its own advantages and disadvantages. We'll explore the most common approaches, applying them to find the LCM of 8, 10, and 15.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120...
By comparing the lists, we can see that the smallest common multiple of 8, 10, and 15 is 120. This method becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
- 15 = 3 x 5
-
Identify the highest power of each prime factor present:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(8, 10, 15) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
This method is more systematic and less prone to error than listing multiples, making it preferable for larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, although the calculation becomes more complex. While we can use this method, it's generally less efficient than prime factorization for finding the LCM of three or more numbers. For the sake of completeness, let's outline the steps:
-
Find the GCD of 8 and 10: Using the Euclidean algorithm, the GCD(8,10) = 2.
-
Find the LCM of 8 and 10: Using the formula: LCM(8, 10) = (8 x 10) / GCD(8,10) = 80 / 2 = 40.
-
Find the GCD of 40 and 15: Using the Euclidean algorithm, the GCD(40,15) = 5.
-
Find the LCM of 40 and 15: LCM(40, 15) = (40 x 15) / GCD(40,15) = 600 / 5 = 120.
Therefore, the LCM(8, 10, 15) = 120. As you can see, this method is more computationally intensive for multiple numbers compared to prime factorization.
Practical Applications of LCM
The concept of LCM has numerous practical applications in various fields:
Scheduling and Timing
Imagine you have three different machines that perform a task at intervals of 8, 10, and 15 minutes, respectively. To determine when all three machines will complete a task simultaneously, you need to find the LCM of 8, 10, and 15, which is 120. Therefore, all machines will complete a task simultaneously every 120 minutes (2 hours).
Fractions and Arithmetic
The LCM is crucial when adding or subtracting fractions with different denominators. To add 1/8 + 1/10 + 1/15, you first find the LCM of 8, 10, and 15 (which is 120), convert each fraction to an equivalent fraction with a denominator of 120, and then perform the addition.
Geometry and Measurement
LCM finds application in geometry when dealing with problems involving lengths, areas, or volumes with different units. Finding a common unit requires determining the LCM of the given units.
Music Theory
In music, the LCM helps determine the least common denominator of different rhythms, facilitating the composition and analysis of musical pieces.
Computer Science
In computer programming and algorithm design, the LCM concept is applied in various tasks such as synchronization of processes or optimizing memory allocation.
Conclusion
Finding the least common multiple is a fundamental skill with broad applicability across various mathematical and real-world scenarios. While multiple methods exist for calculating the LCM, the prime factorization method generally offers the most efficient and reliable approach, especially when dealing with larger numbers or multiple inputs. Understanding the LCM is key to mastering several mathematical concepts and tackling a wide array of practical problems. This guide has provided a comprehensive overview of the concept, its calculation, and its diverse applications, empowering you to confidently apply this essential mathematical tool in your future endeavors. Remember to choose the method that best suits the situation and the complexity of the numbers involved, always prioritizing accuracy and efficiency in your calculations.
Latest Posts
Latest Posts
-
What Is 36 Out Of 40 As A Percentage
May 15, 2025
-
How Much To Tip Dominos Delivery
May 15, 2025
-
Cual Es La Raiz Cuadrada De 1800
May 15, 2025
-
How Many Hours Is 235 Minutes
May 15, 2025
-
Cuantas Son 5 Libras En Kilos
May 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 10 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.