Least Common Multiple Of 4 6 And 7
Treneri
May 14, 2025 · 5 min read
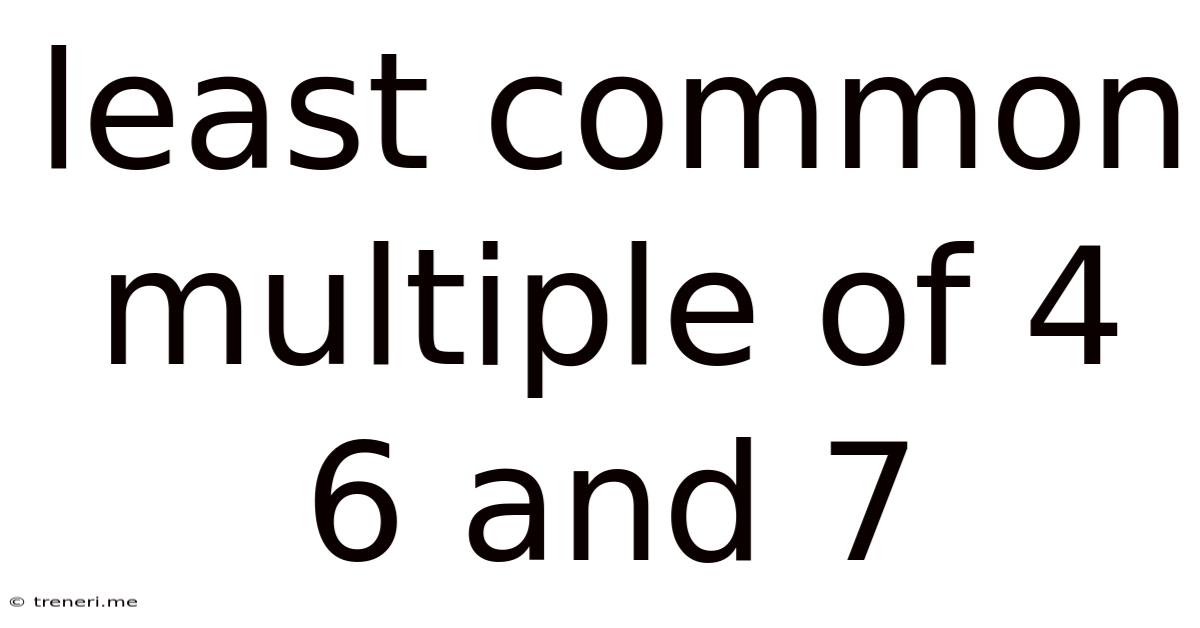
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 7: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with wide-ranging applications, from scheduling problems to simplifying fractions. This comprehensive guide will delve into the process of determining the LCM of 4, 6, and 7, explaining various methods and illustrating their practical applications. We’ll also explore the underlying mathematical principles and offer helpful tips for solving similar problems.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors. This concept is crucial in various mathematical operations, including simplifying fractions and solving problems involving cyclical events.
Method 1: Prime Factorization
This is arguably the most fundamental and conceptually clear method for calculating the LCM. It involves breaking down each number into its prime factors – prime numbers that multiply to give the original number.
Step-by-Step Guide:
-
Prime Factorization of each number:
- 4 = 2 x 2 = 2²
- 6 = 2 x 3
- 7 = 7 (7 is a prime number)
-
Identify the highest power of each prime factor:
- The prime factors present are 2, 3, and 7.
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
-
Multiply the highest powers together:
- LCM(4, 6, 7) = 2² x 3 x 7 = 4 x 3 x 7 = 84
Therefore, the least common multiple of 4, 6, and 7 is 84.
Method 2: Listing Multiples
This method is straightforward but can become cumbersome for larger numbers. It involves listing the multiples of each number until a common multiple is found.
Step-by-Step Guide:
-
List the multiples of each number:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, ...
-
Identify the smallest common multiple:
- Observe that 84 is the smallest number that appears in all three lists.
Therefore, the least common multiple of 4, 6, and 7 is 84.
Method 3: Using the Greatest Common Divisor (GCD)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two or more numbers. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, but the calculation becomes more complex. For three numbers, a more iterative approach is usually preferable. We'll focus on the two-number method and demonstrate how to iteratively apply it.
Step-by-Step Guide:
-
Find the GCD of 4 and 6 using the Euclidean Algorithm:
- 6 = 1 x 4 + 2
- 4 = 2 x 2 + 0
- The GCD(4, 6) is 2.
-
Calculate the LCM of 4 and 6:
- LCM(4, 6) = (4 x 6) / GCD(4, 6) = 24 / 2 = 12
-
Now find the LCM of 12 and 7:
- Since 12 and 7 share no common factors other than 1, their GCD is 1.
- LCM(12, 7) = (12 x 7) / GCD(12, 7) = 84 / 1 = 84
Therefore, the least common multiple of 4, 6, and 7 is 84.
Applications of LCM
The LCM has practical applications in various fields:
-
Scheduling: Determining when events will coincide. For example, if one event occurs every 4 days, another every 6 days, and a third every 7 days, the LCM (84) indicates they will all occur together again after 84 days.
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions. To add 1/4, 1/6, and 1/7, you would need to find a common denominator, which is the LCM(4, 6, 7) = 84.
-
Cyclic Patterns: Identifying when repeating patterns will align. Think of gears turning, or musical rhythms.
-
Number Theory: LCM is a crucial concept in various number theory problems, including modular arithmetic.
Choosing the Right Method
The best method for finding the LCM depends on the numbers involved:
-
Prime Factorization: Most efficient for larger numbers and when understanding the prime factorization is important.
-
Listing Multiples: Simple and intuitive for smaller numbers, but can be time-consuming for larger ones.
-
GCD Method: Efficient if you already know the GCD or need to use the GCD for other calculations. It's particularly helpful when dealing with relatively prime numbers.
Advanced Considerations and Extensions
While we’ve focused on the LCM of three numbers, the concepts extend seamlessly to any number of integers. The prime factorization method remains the most robust approach for handling larger sets of numbers or numbers with many factors. For very large numbers, computational algorithms are employed to efficiently find both the GCD and LCM.
Furthermore, the concepts of LCM and GCD are fundamental building blocks for more advanced mathematical topics, including abstract algebra and cryptography. Understanding these basic principles forms a solid foundation for tackling complex mathematical problems.
Conclusion
Finding the least common multiple of 4, 6, and 7, which is 84, highlights the importance of understanding fundamental mathematical concepts. The various methods discussed offer different approaches depending on the context and the complexity of the problem. Mastering these techniques is crucial for success in various mathematical fields and practical applications. Remember to choose the method that best suits your needs and the complexity of the numbers involved, always aiming for clarity and efficiency in your calculations. The ability to efficiently find LCMs is a valuable skill in various aspects of mathematics and its applications.
Latest Posts
Latest Posts
-
60 Days Before September 30 2024
May 14, 2025
-
How Much Vinyl Flooring Do I Need
May 14, 2025
-
Find My Size By Height And Weight
May 14, 2025
-
Greatest Common Factor Of 6 And 21
May 14, 2025
-
How Many Microns In A Mil
May 14, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 6 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.