Least Common Multiple Of 4 6 And 9
Treneri
May 11, 2025 · 5 min read
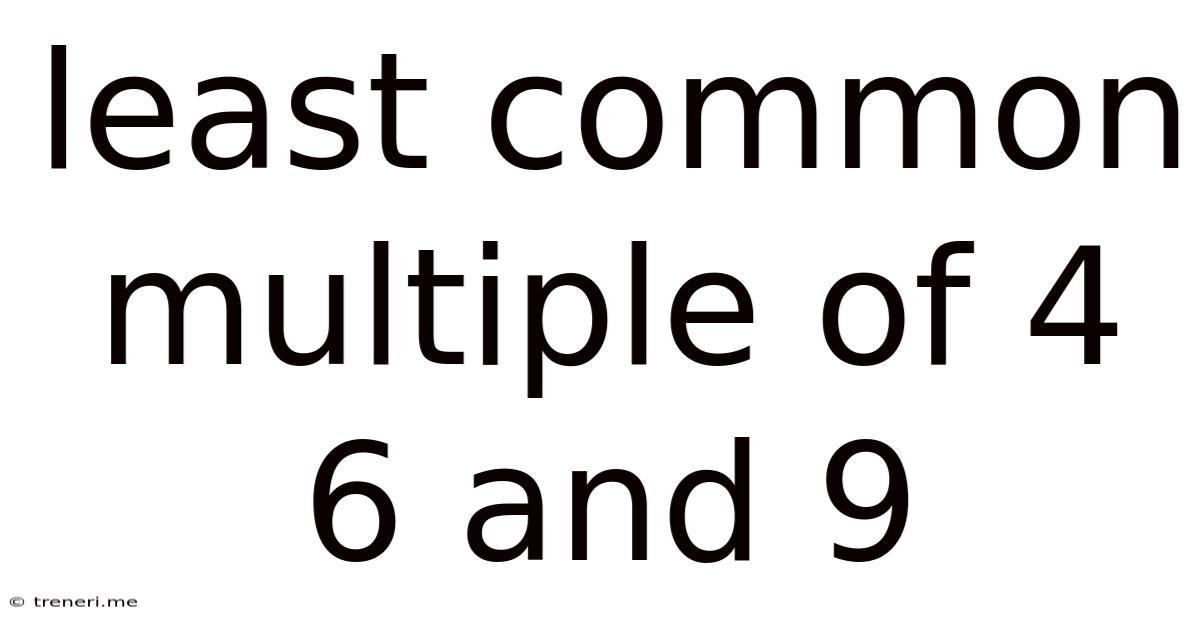
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 9: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex problems in various fields like music theory and scheduling. This article delves into the process of finding the LCM of 4, 6, and 9, explaining multiple methods and providing a deeper understanding of the underlying mathematical principles. We'll explore both manual calculation techniques and how to use this knowledge in real-world scenarios. By the end, you'll not only know the LCM of these three numbers but also possess a solid grasp of LCM calculations in general.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 4, 6, and 9, let's solidify our understanding of the concept. The least common multiple is the smallest positive integer that is a multiple of all the integers in a given set. In simpler terms, it's the smallest number that all the numbers in the set can divide into without leaving a remainder.
Example: Let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
This concept becomes more complex as we add more numbers to the set, as we will see with 4, 6, and 9.
Method 1: Listing Multiples
The most straightforward (though not always the most efficient) method for finding the LCM is by listing the multiples of each number until a common multiple is found.
Step 1: List the multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
Step 2: List the multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48...
Step 3: List the multiples of 9: 9, 18, 27, 36, 45, 54...
Step 4: Identify the smallest common multiple: By comparing the lists, we can see that the smallest number appearing in all three lists is 36.
Therefore, the LCM of 4, 6, and 9 is 36.
While this method is simple for smaller numbers, it becomes cumbersome and time-consuming when dealing with larger numbers. Let's explore more efficient methods.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM, especially when dealing with larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Find the prime factorization of each number:
- 4: 2 x 2 = 2²
- 6: 2 x 3
- 9: 3 x 3 = 3²
Step 2: Identify the highest power of each prime factor: In our factorizations, the prime factors are 2 and 3. The highest power of 2 is 2² (from the factorization of 4), and the highest power of 3 is 3² (from the factorization of 9).
Step 3: Multiply the highest powers together: 2² x 3² = 4 x 9 = 36
Therefore, the LCM of 4, 6, and 9 is 36. This method is significantly more efficient than listing multiples, especially for larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides all the numbers in a set without leaving a remainder. There's a formula that connects the LCM and GCD:
LCM(a, b, c) * GCD(a, b, c) = a * b * c
While this formula is generally used for two numbers, we can adapt it for three or more numbers by applying it iteratively. First, we find the LCM of two numbers, and then find the LCM of that result and the third number. Let's use this method to find the LCM of 4, 6, and 9:
Step 1: Find the GCD of 4 and 6 using the Euclidean algorithm:
- 6 = 1 * 4 + 2
- 4 = 2 * 2 + 0
The GCD of 4 and 6 is 2.
Step 2: Find the LCM of 4 and 6 using the formula:
LCM(4, 6) * GCD(4, 6) = 4 * 6 LCM(4, 6) * 2 = 24 LCM(4, 6) = 12
Step 3: Find the GCD of 12 and 9:
- 12 = 1 * 9 + 3
- 9 = 3 * 3 + 0
The GCD of 12 and 9 is 3.
Step 4: Find the LCM of 12 and 9 using the formula:
LCM(12, 9) * GCD(12, 9) = 12 * 9 LCM(12, 9) * 3 = 108 LCM(12, 9) = 36
Therefore, the LCM of 4, 6, and 9 is 36. This method demonstrates the interconnectedness of LCM and GCD.
Real-World Applications of LCM
The concept of LCM extends far beyond theoretical mathematics; it finds practical applications in diverse fields:
-
Scheduling: Imagine you have three tasks – one taking 4 hours, another 6 hours, and a third 9 hours. The LCM (36) represents the shortest time after which all three tasks will finish simultaneously.
-
Music: The LCM is crucial in music theory for determining the least common multiple of note durations, helping composers create harmonious and rhythmically consistent compositions.
-
Pattern Recognition: LCM helps in identifying repeating patterns or cycles. For example, if three lights blink at intervals of 4, 6, and 9 seconds respectively, they will all blink together after 36 seconds.
-
Fraction Operations: Finding a common denominator when adding or subtracting fractions involves calculating the LCM of the denominators. This ensures that the fractions are expressed with a common base, simplifying the addition/subtraction process.
-
Engineering: In manufacturing and engineering processes, the LCM plays a role in coordinating machine cycles and optimizing production lines to achieve efficient synchronization.
Conclusion
Calculating the least common multiple of 4, 6, and 9, as demonstrated above, highlights the importance of understanding fundamental mathematical concepts. While listing multiples provides a basic approach, the prime factorization method offers a more efficient and scalable solution for larger numbers. The relationship between LCM and GCD further enhances our mathematical toolkit. The practical applications of the LCM across various fields underline its significance beyond abstract mathematical exercises. Mastering the calculation of the LCM empowers you to tackle complex problems efficiently and understand the underlying patterns in various real-world scenarios. Remember that consistent practice and a thorough understanding of the underlying principles will lead to mastery of this essential mathematical concept.
Latest Posts
Latest Posts
-
43 27 An Hour Is How Much A Year
May 11, 2025
-
How Much Soil Do I Need For Lawn
May 11, 2025
-
5 Gallons Is Equal To How Many Pints
May 11, 2025
-
5 Pies 6 Pulgadas A Metros
May 11, 2025
-
How Do You Measure A Phone Screen
May 11, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 6 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.