Negative Two-thirds Times A Number Is At Least 12.
Treneri
May 14, 2025 · 5 min read
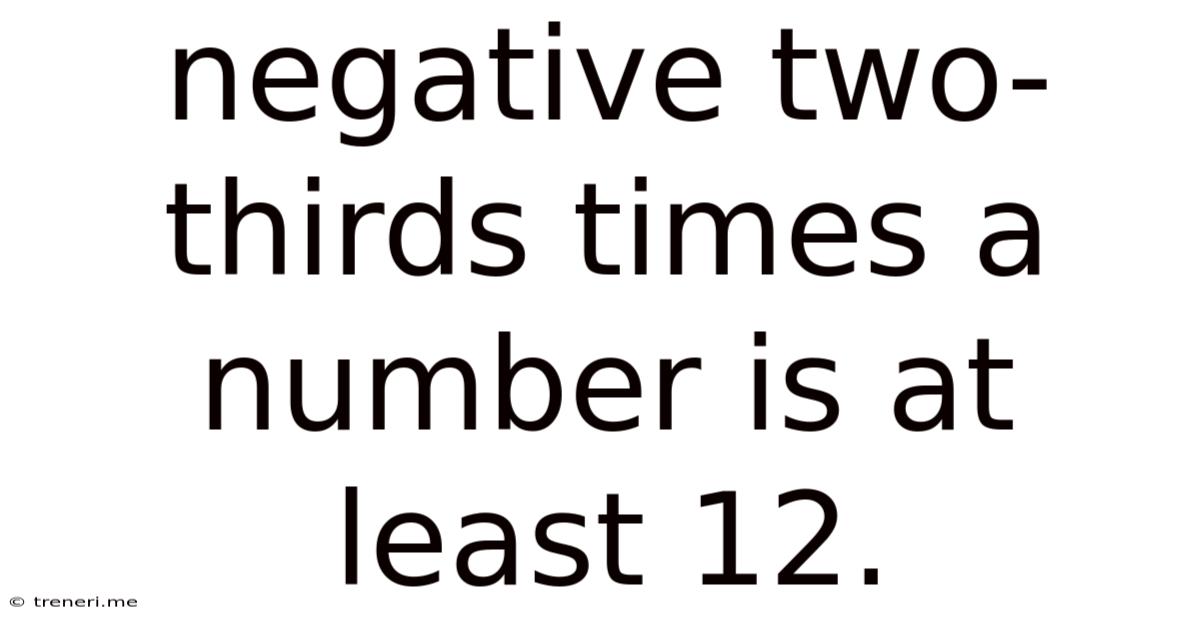
Table of Contents
Negative Two-Thirds Times a Number is at Least 12: A Comprehensive Exploration
This article delves into the mathematical inequality "-⅔x ≥ 12," exploring its solution, interpretation, and practical applications. We'll break down the problem step-by-step, offering a clear understanding for students and anyone interested in sharpening their algebra skills. We'll also discuss the broader context of inequalities and their relevance in real-world scenarios.
Understanding the Inequality: -⅔x ≥ 12
The inequality "-⅔x ≥ 12" presents a mathematical statement indicating that negative two-thirds of a certain number ('x') is greater than or equal to 12. This isn't simply an equation with a single solution; instead, it represents a range of possible values for 'x'. Let's dissect this further:
- -⅔: This represents a negative fraction, indicating a reduction or decrease.
- x: This is the unknown variable we aim to solve for.
- ≥: This symbol denotes "greater than or equal to," meaning the expression on the left (-⅔x) can be equal to 12 or greater than 12.
Solving the Inequality
Solving this inequality involves manipulating it algebraically to isolate 'x'. The process involves carefully considering the impact of multiplying or dividing by negative numbers.
Step 1: Multiplying Both Sides by -3/2
To eliminate the fraction (-⅔) attached to 'x', we multiply both sides of the inequality by its reciprocal, -3/2. Crucially, because we are multiplying by a negative number, we must reverse the inequality sign.
(-⅔x) * (-3/2) ≥ 12 * (-3/2)
This simplifies to:
x ≤ -18
Step 2: Understanding the Solution
The solution, x ≤ -18, means that any number less than or equal to -18 satisfies the original inequality. This represents an infinite set of solutions. Let's test this with a few examples:
- x = -18: (-⅔)(-18) = 12. This satisfies the inequality.
- x = -20: (-⅔)(-20) = 40/3 ≈ 13.33. This also satisfies the inequality.
- x = -10: (-⅔)(-10) = 20/3 ≈ 6.67. This does not satisfy the inequality.
These examples confirm that only values of 'x' less than or equal to -18 fulfill the condition "-⅔x ≥ 12."
Graphical Representation
Inequalities can be visually represented on a number line. For x ≤ -18:
- Draw a number line.
- Locate -18 on the number line.
- Draw a closed circle (or a filled-in dot) at -18, indicating that -18 is included in the solution.
- Shade the region to the left of -18, representing all numbers less than -18.
This visual representation provides a clear and concise summary of the solution set.
Real-World Applications
While this might seem like an abstract mathematical problem, inequalities like this appear frequently in real-world situations. Consider these examples:
1. Budgeting and Expenses
Imagine you're managing a budget and want to ensure your expenses don't exceed a certain limit. Let's say you're aiming to keep your monthly entertainment spending to no more than $100. Suppose you spend two-thirds of your entertainment budget on dining out. The inequality could represent this scenario:
-(⅔)x ≥ -100 (where 'x' is your total entertainment budget)
Solving this, we'd find the minimum entertainment budget you need to remain within your limit.
2. Temperature Changes
Consider a scenario where temperature decreases at a consistent rate. If the temperature decreases by two-thirds of a degree every hour and needs to reach at least 12 degrees below a certain point, the inequality can model this scenario to determine the minimum starting temperature.
3. Production and Sales
Suppose a company produces items at a cost that represents two-thirds of the selling price. If they want their profit to be at least $12 per item, they can model this situation using an inequality to find the minimum selling price per item.
Expanding on Inequalities: Key Concepts
Understanding the solution to "-⅔x ≥ 12" requires a grasp of broader concepts within inequalities:
1. Inequality Symbols
Familiarize yourself with the different inequality symbols:
- >: Greater than
- <: Less than
- ≥: Greater than or equal to
- ≤: Less than or equal to
These symbols are crucial for accurately representing and solving inequalities.
2. Solving Compound Inequalities
Sometimes, you'll encounter compound inequalities, which involve more than one inequality symbol. For example:
-5 < 2x + 3 ≤ 11
Solving these requires isolating 'x' while maintaining the relationships between the different parts of the inequality.
3. Absolute Value Inequalities
Absolute value inequalities involve the absolute value function (| |), which represents the distance of a number from zero. Solving these requires considering both positive and negative cases. For example:
|x| > 5
This means x > 5 or x < -5.
4. Graphing Inequalities
As demonstrated earlier, graphing inequalities on a number line provides a visual representation of the solution set. Understanding how to graph inequalities is essential for interpreting results and understanding the range of possible solutions.
5. Applications in Calculus and Advanced Mathematics
Inequalities form a foundational concept in more advanced mathematical fields such as calculus, where they are used extensively in optimization problems and the study of functions.
Conclusion: Mastering Inequalities
The seemingly simple inequality "-⅔x ≥ 12" serves as a gateway to a deeper understanding of inequalities and their widespread applications. By carefully considering the steps involved in solving the inequality, understanding the solution, and exploring its visual representation, we gain valuable insights into mathematical reasoning and its practical relevance. This knowledge extends beyond basic algebra, forming a solid foundation for more complex mathematical concepts and real-world problem-solving. The ability to translate real-world scenarios into mathematical inequalities is a powerful tool for anyone seeking to analyze data, make predictions, and optimize outcomes. Mastering these concepts opens doors to a broader understanding of quantitative analysis and its role in diverse fields.
Latest Posts
Latest Posts
-
How Many Days Is 338 Hours
May 14, 2025
-
How Long Does It Take To Be Tan
May 14, 2025
-
Cuantos Dias Faltan Para El 24 De Septiembre
May 14, 2025
-
How Many Hours Is 15000 Seconds
May 14, 2025
-
How Many Quarts Are In 6 Cups
May 14, 2025
Related Post
Thank you for visiting our website which covers about Negative Two-thirds Times A Number Is At Least 12. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.