Square Root Of Negative 1 Divided By 8
Treneri
May 13, 2025 · 5 min read
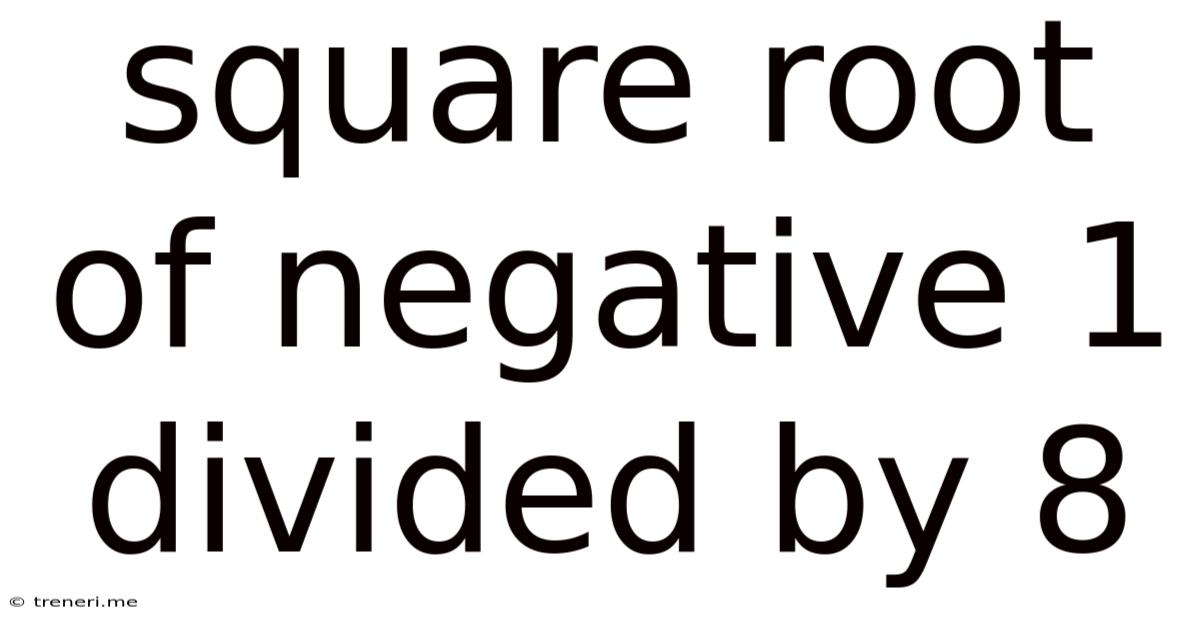
Table of Contents
Delving into the Depths: Exploring √(-1)/8
The expression √(-1)/8, seemingly simple at first glance, opens a fascinating window into the world of complex numbers. While the square root of a negative number might initially seem paradoxical within the realm of real numbers, its exploration reveals a rich mathematical landscape with significant applications across various scientific and engineering fields. This article delves deep into understanding this expression, exploring its fundamental components, its representation, and its implications.
Understanding the Fundamentals: Real and Complex Numbers
Before we tackle √(-1)/8, let's establish a firm foundation in number systems. We're all familiar with real numbers – the numbers we use in everyday life, including positive numbers, negative numbers, and zero. These numbers can be plotted on a number line. However, the square root of a negative number, such as √(-1), doesn't exist within the real number system. This is because no real number, when multiplied by itself, yields a negative result.
This limitation led to the expansion of the number system to include complex numbers. Complex numbers are numbers of the form a + bi, where:
- 'a' is the real part of the complex number.
- 'b' is the imaginary part of the complex number.
- 'i' is the imaginary unit, defined as √(-1).
The introduction of the imaginary unit, i, allows us to express the square root of negative numbers. For example, √(-9) can be written as √(9 * -1) = √(9) * √(-1) = 3i.
Deconstructing √(-1)/8: A Step-by-Step Approach
Now, let's dissect our expression, √(-1)/8. We can rewrite this as:
√(-1) / 8 = i / 8
This simplification reveals that the expression is simply the imaginary unit, i, divided by 8. This represents a complex number where the real part is 0, and the imaginary part is 1/8. We can write this in the standard form of a complex number as:
0 + (1/8)i
This form clearly illustrates that the expression represents a point in the complex plane, specifically at a distance of 1/8 along the positive imaginary axis.
Visualizing Complex Numbers: The Complex Plane
The complex plane (Argand plane) provides a powerful visual tool for understanding complex numbers. The horizontal axis represents the real part of the complex number, and the vertical axis represents the imaginary part. Our expression, 0 + (1/8)i, is plotted as a point at (0, 1/8) on the complex plane. This visualization allows us to grasp the magnitude and direction of the complex number.
Magnitude and Argument (Polar Form): A Deeper Dive
Beyond the Cartesian representation (0, 1/8), complex numbers can also be expressed in polar form, using magnitude (or modulus) and argument (or phase).
-
Magnitude (r): This represents the distance of the point from the origin (0,0) in the complex plane. For our expression, the magnitude is calculated as: r = √(0² + (1/8)²) = 1/8
-
Argument (θ): This represents the angle the line connecting the point to the origin makes with the positive real axis. In our case, the point lies on the positive imaginary axis, meaning the angle is 90 degrees or π/2 radians.
Therefore, the polar form of √(-1)/8 is (1/8, π/2) or (1/8, 90°). This form provides an alternative perspective on the complex number, highlighting its distance from the origin and its orientation.
Operations with Complex Numbers Involving √(-1)/8
Understanding the nature of √(-1)/8 allows us to perform various mathematical operations involving this expression. For example, consider adding it to another complex number:
(2 + 3i) + (0 + (1/8)i) = 2 + (25/8)i
Similarly, multiplication and division with other complex numbers are feasible. For instance:
(2 + 3i) * (0 + (1/8)i) = (2 * 0) + (2 * (1/8)i) + (3i * 0) + (3i * (1/8)i) = (3/8)i² + (1/4)i = -(3/8) + (1/4)i
These examples illustrate how smoothly √(-1)/8 integrates with the broader field of complex arithmetic.
Applications in Science and Engineering
Complex numbers, and hence expressions like √(-1)/8, are not merely abstract mathematical concepts. They find extensive application in various scientific and engineering disciplines:
-
Electrical Engineering: Complex numbers are essential for analyzing alternating current (AC) circuits. Impedance, a measure of opposition to current flow, is often expressed as a complex number.
-
Signal Processing: Complex numbers are crucial in representing and manipulating signals, enabling tasks like filtering, modulation, and demodulation.
-
Quantum Mechanics: The mathematical framework of quantum mechanics heavily relies on complex numbers to describe the wave function of particles.
-
Fluid Dynamics: Complex numbers simplify the mathematical descriptions of fluid flow, particularly in analyzing potential flow around objects.
-
Control Systems: Complex numbers are used in the analysis and design of control systems, assisting in stabilizing systems and optimizing performance.
These are just a few examples of the widespread utility of complex numbers across diverse scientific and engineering fields. Understanding the basics, as demonstrated with our exploration of √(-1)/8, is fundamental to comprehending these applications.
Advanced Concepts: Exponential and Trigonometric Forms
Complex numbers can also be represented in exponential form (Euler's formula) and trigonometric form. These forms offer further insights into the properties of complex numbers and are particularly useful in advanced mathematical operations.
Exponential Form: Using Euler's formula, e^(iθ) = cos(θ) + i sin(θ), our complex number can be represented as:
(1/8)e^(iπ/2)
Trigonometric Form: The trigonometric form directly utilizes the magnitude and argument:
r(cos(θ) + i sin(θ)) = (1/8)(cos(π/2) + i sin(π/2))
These advanced representations offer alternative ways to perform calculations and reveal deeper properties of the complex number, including its relationship to rotations and oscillations.
Conclusion: A Simple Expression, a Profound Impact
While √(-1)/8 might appear as a simple mathematical expression, its exploration unveils a gateway to the fascinating world of complex numbers. From its representation on the complex plane to its practical applications across various scientific and engineering disciplines, its significance extends far beyond its initial appearance. Understanding this seemingly simple expression provides a stepping stone to mastering the intricacies of complex numbers and their profound impact on our understanding of the world around us. The journey from real numbers to the complex plane, as highlighted by this expression, illustrates the power of mathematical expansion and the beauty of abstract mathematical concepts finding practical, tangible applications in the real world. Further exploration of complex analysis will reveal even more profound implications and applications of this seemingly simple expression.
Latest Posts
Latest Posts
-
What Is The Volume Of The Cylinder Shown
May 14, 2025
-
15 Is 70 Percent Of What Number
May 14, 2025
-
129 Rounded To The Nearest Hundred
May 14, 2025
-
How Many Cups Are In 18 Pints
May 14, 2025
-
How To Find Sides Of Triangle With Only Angles
May 14, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of Negative 1 Divided By 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.