The Volume Of A 9 Inch Cube Is
Treneri
Apr 05, 2025 · 6 min read
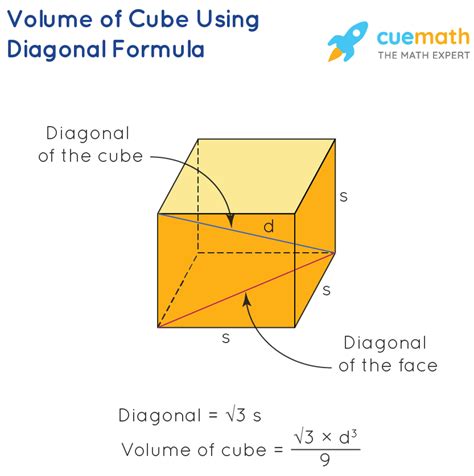
Table of Contents
The Volume of a 9-Inch Cube: A Comprehensive Exploration
The seemingly simple question, "What is the volume of a 9-inch cube?" opens a door to a fascinating exploration of geometry, its practical applications, and the importance of understanding three-dimensional space. While the answer itself is straightforward, delving deeper reveals a wealth of knowledge relevant to various fields, from architecture and engineering to data analysis and even theoretical physics. This article will not only provide the answer but also explore the concept of volume, its calculation for cubes and other shapes, and its significance in various contexts.
Understanding Volume: A Foundation in Three Dimensions
Before diving into the specifics of a 9-inch cube, let's establish a firm understanding of the concept of volume. Volume, in simple terms, is the amount of three-dimensional space occupied by an object. It's a measure of how much space something takes up. Unlike area, which is a two-dimensional measurement (length x width), volume incorporates a third dimension: height or depth. This means we need three measurements to calculate the volume of a three-dimensional object.
The units of volume are always cubic units (e.g., cubic inches, cubic centimeters, cubic meters), reflecting the three-dimensional nature of the measurement. This is because we're multiplying three lengths together: length x width x height.
Different Shapes, Different Formulas
While the formula for the volume of a cube is relatively simple, calculating the volume of other shapes requires different approaches. For instance:
- Rectangular Prism (Cuboid): Volume = Length x Width x Height. This is a generalization of the cube, where the lengths of the sides can be different.
- Sphere: Volume = (4/3)πr³, where 'r' is the radius. This formula involves pi (π), a mathematical constant approximately equal to 3.14159.
- Cylinder: Volume = πr²h, where 'r' is the radius and 'h' is the height.
- Cone: Volume = (1/3)πr²h, where 'r' is the radius and 'h' is the height.
These diverse formulas highlight the importance of understanding the specific shape when calculating volume. Incorrectly applying a formula can lead to significant errors.
Calculating the Volume of a 9-Inch Cube
Now, let's address the central question: what is the volume of a 9-inch cube? A cube is a special type of rectangular prism where all three dimensions (length, width, and height) are equal. Therefore, the volume of a cube is simply the length of one side cubed (side x side x side, or side³).
In the case of a 9-inch cube, the volume is calculated as follows:
Volume = 9 inches x 9 inches x 9 inches = 729 cubic inches
Therefore, the volume of a 9-inch cube is 729 cubic inches. This simple calculation demonstrates the fundamental principle of volume calculation for cubes.
Practical Applications of Cube Volume Calculations
Understanding how to calculate the volume of a cube has numerous practical applications across various fields:
- Packaging and Shipping: Companies need to determine the volume of boxes to optimize shipping costs and ensure efficient packing of goods. Understanding cubic volume helps determine the number of items that can fit into a container.
- Construction and Engineering: Volume calculations are crucial in construction for determining the amount of materials needed, such as concrete for foundations or soil for landscaping projects.
- Manufacturing: In manufacturing, volume calculations are essential for designing molds, determining the capacity of containers, and optimizing production processes.
- Medicine and Pharmacy: Volume calculations are critical in pharmacy for precise medication dosages and in medical imaging for determining the size and volume of organs or tumors.
These examples highlight the pervasive nature of volume calculations in everyday life and professional settings. The ability to accurately calculate volume ensures efficiency, accuracy, and cost-effectiveness in numerous endeavors.
Beyond the Basics: Exploring Related Concepts
The concept of volume extends beyond simple cube calculations. Several related concepts build upon this fundamental understanding:
Surface Area
While volume measures the space inside a three-dimensional object, surface area measures the total area of its outer surfaces. For a cube, the surface area is calculated by finding the area of each face (side x side) and multiplying by 6 (since a cube has six faces). For our 9-inch cube, the surface area would be 6 x (9 inches x 9 inches) = 486 square inches. Understanding both volume and surface area is crucial in many applications, such as minimizing material use while maximizing internal space.
Density
Density relates mass and volume. It's defined as mass per unit volume (Density = Mass/Volume). Knowing the volume of an object allows us to calculate its density if we know its mass, and vice versa. Density is an important physical property used to identify substances and understand their behavior.
Units of Measurement
Consistent use of units is crucial in all volume calculations. Failing to use the correct units can lead to significant errors. Conversion between units (e.g., cubic inches to cubic feet, cubic centimeters to liters) is a common task requiring careful attention to detail.
Advanced Applications
The concepts of volume and three-dimensional space extend into more complex mathematical and scientific fields. Calculus, for example, uses integration to calculate volumes of irregular shapes that cannot be easily calculated using simple geometric formulas. In fields like fluid dynamics and thermodynamics, volume plays a critical role in understanding the behavior of liquids and gases.
Mastering Volume Calculations: Tips and Tricks
Mastering volume calculations, especially for cubes and other simple shapes, requires practice and attention to detail. Here are some tips:
- Visualize the Shape: Before starting any calculation, visualize the shape in your mind's eye. This helps to ensure you're using the correct formula and understanding the dimensions.
- Identify the Relevant Formula: Carefully select the correct formula based on the shape of the object. Using the wrong formula will result in an incorrect answer.
- Use Consistent Units: Always use consistent units throughout your calculation. Converting units at the end can be error-prone.
- Check Your Work: After completing the calculation, review your work to ensure accuracy. A simple mistake can significantly affect the final result.
- Practice Regularly: The best way to master volume calculations is through consistent practice. Work through various examples using different shapes and units.
Conclusion: The Enduring Significance of Volume
The seemingly simple question of the volume of a 9-inch cube opens a gateway to a vast and fascinating world of geometry, mathematics, and its practical applications across numerous disciplines. From the everyday tasks of packaging and construction to the complexities of scientific research, understanding volume is fundamental to accurate measurement, efficient design, and insightful analysis. By mastering the principles of volume calculation, individuals equip themselves with a powerful tool applicable across various aspects of life and work. Remember that consistent practice, careful attention to detail, and a firm grasp of the underlying concepts are crucial to achieving mastery in this essential area of mathematics. The 729 cubic inches of our 9-inch cube represent not just a numerical answer, but a testament to the enduring power and relevance of fundamental geometric principles.
Latest Posts
Latest Posts
-
24 Oz Is How Many Grams
Apr 06, 2025
-
1 Tablespoon Of Minced Garlic To Garlic Powder
Apr 06, 2025
-
Cuanto Es 200 Gramos En Onzas
Apr 06, 2025
-
How Much More Days Until Valentines Day
Apr 06, 2025
-
Vickers Hardness To Rockwell C Conversion
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about The Volume Of A 9 Inch Cube Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
