Three Fractions That Are Equal To 4/12
Treneri
May 10, 2025 · 5 min read
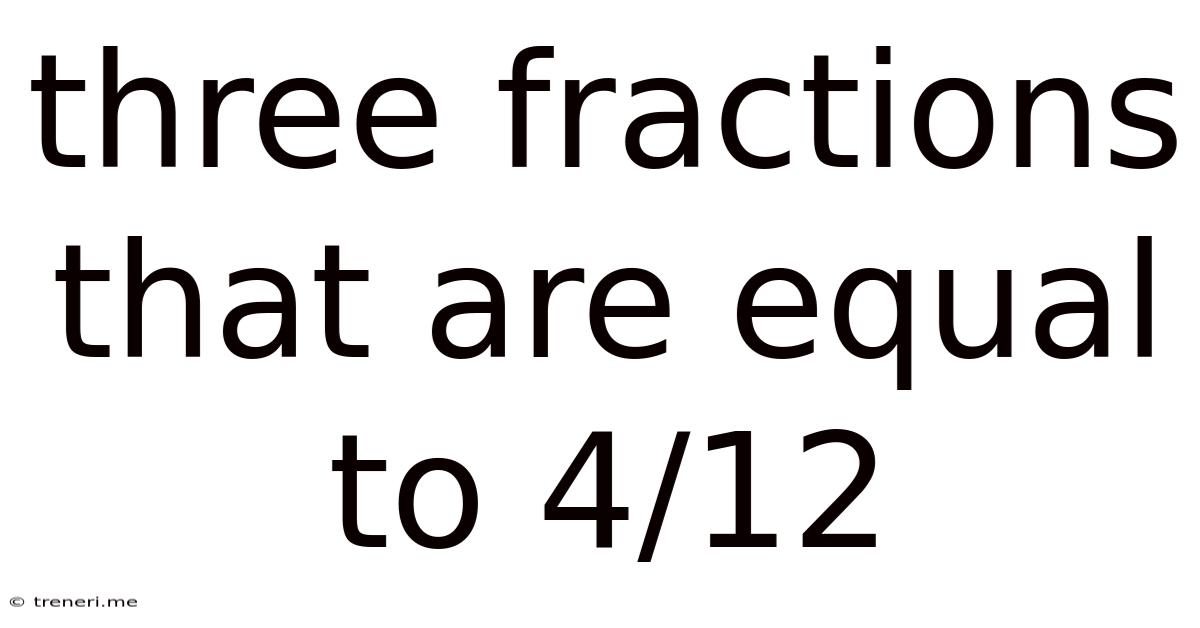
Table of Contents
Three Fractions Equal to 4/12: A Deep Dive into Equivalent Fractions
Finding fractions equivalent to a given fraction is a fundamental concept in mathematics. Understanding this concept is crucial for mastering various mathematical operations, from simplifying expressions to solving complex equations. This article will explore three fractions equal to 4/12, delving into the underlying principles and providing a comprehensive understanding of equivalent fractions. We'll also touch upon the practical applications of this concept and address common misconceptions.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. Think of a pizza cut into 12 slices. 4/12 represents four out of twelve slices. An equivalent fraction would represent the same amount of pizza, just with a different number of slices. The key to finding equivalent fractions lies in the concept of simplification and multiplication.
The Fundamental Principle: Multiplying the Numerator and Denominator by the Same Number
The core principle behind finding equivalent fractions is to multiply both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number. This operation maintains the ratio between the numerator and denominator, thus preserving the value of the fraction.
For example, if we multiply both the numerator and denominator of 4/12 by 2, we get:
(4 * 2) / (12 * 2) = 8/24
8/24 is an equivalent fraction to 4/12. They both represent the same portion – one-third. We can visualize this: imagine two pizzas, one cut into 12 slices and the other into 24. If you take 4 slices from the first pizza and 8 slices from the second, you've consumed the same amount of pizza.
The Reverse Process: Simplifying Fractions
The reverse process of finding equivalent fractions is simplifying, also known as reducing to lowest terms. This involves dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's take 4/12 again. The GCD of 4 and 12 is 4. Dividing both by 4 gives us:
4 / 4 = 1
12 / 4 = 3
Therefore, the simplified form of 4/12 is 1/3. This is the simplest form of the fraction, as the numerator and denominator have no common factors other than 1.
Three Fractions Equal to 4/12
Now, let's find three fractions that are equal to 4/12. We can achieve this by multiplying the numerator and denominator by different non-zero numbers.
1. 8/24: As demonstrated earlier, multiplying both 4 and 12 by 2 gives us 8/24. This is one equivalent fraction.
2. 6/18: Multiplying both the numerator and denominator of 4/12 by 3/2 gives us 6/18. This demonstrates that we don't need to use only whole numbers to generate equivalent fractions.
3. 12/36: Multiplying both 4 and 12 by 3 results in 12/36. This fraction, while appearing different, represents the same proportion as 4/12 and 1/3.
These three fractions (8/24, 6/18, and 12/36) are all equivalent to 4/12. They all simplify to 1/3. This illustrates the infinite number of equivalent fractions that can be generated for any given fraction.
Visualizing Equivalent Fractions
Visual representations can significantly aid in understanding equivalent fractions. Consider the following:
-
Area Models: Draw a rectangle and divide it into 12 equal parts. Shade 4 of these parts to represent 4/12. Then, draw another rectangle of the same size and divide it into 24 equal parts. Shade 8 of these parts. You'll observe that the shaded areas are identical in both rectangles, demonstrating the equivalence of 4/12 and 8/24. This approach can be applied to other equivalent fractions as well.
-
Number Lines: Draw a number line from 0 to 1. Mark the fractions 4/12, 8/24, 6/18, and 12/36. You'll find that all these fractions fall on the same point on the number line, reinforcing their equivalence.
Applications of Equivalent Fractions
The concept of equivalent fractions has extensive applications in various areas:
-
Simplifying algebraic expressions: Equivalent fractions are often used to simplify complex fractions and expressions, making them easier to manipulate and solve.
-
Solving equations: When solving equations involving fractions, finding equivalent fractions can be essential for finding a common denominator, enabling the addition or subtraction of fractions.
-
Measurement and conversion: Converting between different units of measurement often involves working with equivalent fractions. For example, converting inches to feet involves using equivalent fractions.
-
Proportions and ratios: Equivalent fractions play a crucial role in understanding and solving problems involving proportions and ratios in various fields, including cooking, engineering, and science.
-
Percentage calculations: Percentages are essentially fractions with a denominator of 100. Finding equivalent fractions is often necessary when converting between percentages and fractions or decimals.
Common Misconceptions about Equivalent Fractions
-
Adding numerators and denominators: A common mistake is adding the numerators and denominators separately to find equivalent fractions. This is incorrect. Remember, you must multiply both the numerator and denominator by the same number.
-
Confusing simplification with finding equivalent fractions: While simplification is the reverse process of finding equivalent fractions, they are distinct operations. Simplifying aims to reduce a fraction to its lowest terms, while finding equivalent fractions aims to generate fractions with different numerators and denominators but the same value.
Conclusion
Understanding equivalent fractions is a fundamental skill in mathematics. By mastering the principle of multiplying or dividing both the numerator and denominator by the same number, you can confidently find an infinite number of equivalent fractions for any given fraction. This knowledge extends to numerous mathematical applications, enhancing your problem-solving abilities and providing a solid foundation for more advanced mathematical concepts. Remember to practice regularly and visualize the concept using area models and number lines to fully grasp its significance. By embracing the practical applications and avoiding common misconceptions, you'll build a robust understanding of equivalent fractions that will benefit you throughout your mathematical journey. The three examples provided—8/24, 6/18, and 12/36—illustrate just a small fraction (pun intended!) of the possibilities. Continue exploring and you'll uncover the rich world of equivalent fractions.
Latest Posts
Latest Posts
-
How Many Weeks Are In 32 Days
May 10, 2025
-
How Many Calories Are In A Chocolate
May 10, 2025
-
Circumference Of A 15 Foot Circle
May 10, 2025
-
Formula For Finding The Base Of A Triangle
May 10, 2025
-
Born In 1996 How Old In 2023
May 10, 2025
Related Post
Thank you for visiting our website which covers about Three Fractions That Are Equal To 4/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.