What Are The Factors Of 92
Treneri
Apr 07, 2025 · 5 min read
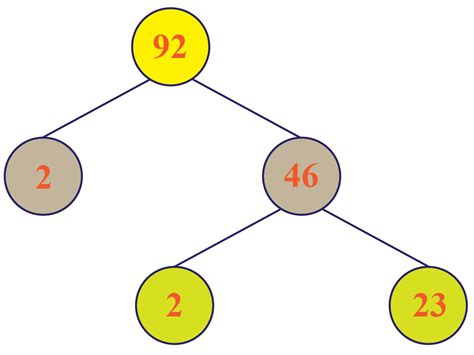
Table of Contents
Unraveling the Factors of 92: A Deep Dive into Number Theory
The seemingly simple question, "What are the factors of 92?", opens a door to a fascinating world of number theory. While the immediate answer might seem straightforward, exploring the concept of factors, their properties, and the methods for finding them reveals a rich mathematical landscape. This article delves deep into the factors of 92, explaining not only the answer but also the underlying mathematical principles, practical applications, and connections to broader mathematical concepts.
Understanding Factors and Divisibility
Before we tackle the specific factors of 92, let's establish a firm understanding of fundamental concepts. A factor (or divisor) of a number is a whole number that divides that number exactly, leaving no remainder. In other words, if 'a' is a factor of 'b', then b/a results in a whole number. Divisibility rules offer shortcuts to determine factors quickly, but the underlying principle is always whole-number division without a remainder.
Finding the Factors of 92: A Step-by-Step Approach
There are several ways to find the factors of 92. Let's explore a few methods, each offering unique insights:
1. The Brute Force Method: This involves systematically checking each whole number from 1 up to 92 to see if it divides 92 without a remainder. While straightforward, it becomes inefficient for larger numbers.
2. Prime Factorization: This is a more elegant and efficient method. Prime factorization involves expressing a number as the product of its prime factors – numbers that are only divisible by 1 and themselves. Finding the prime factorization of 92 provides a complete picture of its factors.
Let's perform the prime factorization of 92:
- 92 is an even number, so it's divisible by 2: 92 = 2 x 46
- 46 is also even, so it's divisible by 2: 46 = 2 x 23
- 23 is a prime number.
Therefore, the prime factorization of 92 is 2 x 2 x 23, or 2² x 23.
3. Pairwise Identification: Once we have the prime factorization (2² x 23), we can systematically generate all possible factors. We consider all combinations of the prime factors:
- 2¹ = 2
- 2² = 4
- 2³ = 8 (Not a factor directly, since 92/8=11.5; however, this explains why 8 is not in the factors)
- 23¹ = 23
- 2¹ x 23¹ = 46
- 2² x 23¹ = 92
- 1 (Every number is divisible by 1)
Therefore, the factors of 92 are: 1, 2, 4, 23, 46, and 92.
Understanding the Significance of Factors
The factors of a number hold significant importance in various mathematical contexts:
-
Greatest Common Divisor (GCD): Factors are crucial in finding the GCD of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder. For example, finding the GCD of 92 and another number would involve comparing their factors.
-
Least Common Multiple (LCM): Factors play a role in calculating the LCM, which is the smallest number that is a multiple of all the given numbers.
-
Number Theory: Factors are fundamental in number theory, a branch of mathematics concerned with the properties of integers. Concepts like perfect numbers (where the sum of the factors equals the number itself), abundant numbers (sum of factors > number), and deficient numbers (sum of factors < number) all rely heavily on understanding factors.
-
Algebra: Factoring is a vital technique in algebra for simplifying expressions and solving equations. Understanding factors allows us to rewrite expressions in a more manageable form.
-
Cryptography: Factorization, particularly the difficulty of factoring very large numbers into their prime factors, forms the basis of many modern cryptographic systems. The security of these systems depends on the computational difficulty of this task.
Exploring Further: Connections to Other Mathematical Concepts
The concept of factors extends far beyond simply listing the divisors of a number. It's intricately connected to many other mathematical concepts:
-
Modular Arithmetic: Modular arithmetic deals with remainders after division. Factors are inherently linked to modular arithmetic because a number is a factor if and only if the remainder is 0 when dividing.
-
Divisibility Rules: Rules of divisibility provide quick tests to determine whether a number is divisible by another (and therefore, if one number is a factor of the other). These rules are shortcuts based on the properties of the number system.
-
Euclidean Algorithm: The Euclidean algorithm is an efficient method for computing the GCD of two numbers. This algorithm relies heavily on the concept of factors and division.
Practical Applications of Factors
Beyond the purely theoretical, understanding factors has practical applications in various fields:
-
Data Structures: In computer science, factors are relevant in optimizing data structures and algorithms. Efficient algorithms often exploit the properties of factors and divisibility.
-
Engineering: In engineering design, understanding divisibility and factors is important in tasks such as evenly distributing loads or dividing resources.
-
Scheduling and Planning: Factors play a role in scheduling tasks, allocating resources, and planning projects where efficient division of work is critical.
Conclusion: The Enduring Importance of Factors
The factors of 92, seemingly a simple arithmetical exercise, provide a gateway to a deeper understanding of number theory and its wide-ranging applications. By exploring the different methods for finding factors, their significance in various mathematical concepts, and their practical applications, we appreciate the profound impact of this seemingly simple idea. The journey from identifying the factors of 92 to understanding its connections to complex mathematical concepts illustrates the beauty and interconnectedness of mathematics. It's a testament to the power of seemingly simple ideas to unlock a world of mathematical discovery. Further exploration into these topics will reveal even more intricacies and practical applications of factorization, reinforcing its enduring importance in the mathematical landscape.
Latest Posts
Latest Posts
-
How Much Time Until 9 Am
Apr 08, 2025
-
How To Find The Square Foot Of A Rectangle
Apr 08, 2025
-
Elliptical Trainer How Many Calories Burned
Apr 08, 2025
-
2 5 To The Power Of 3
Apr 08, 2025
-
How Many Weeks In 18 Years
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 92 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.