What Fraction Is Equal To 2 5
Treneri
May 10, 2025 · 5 min read
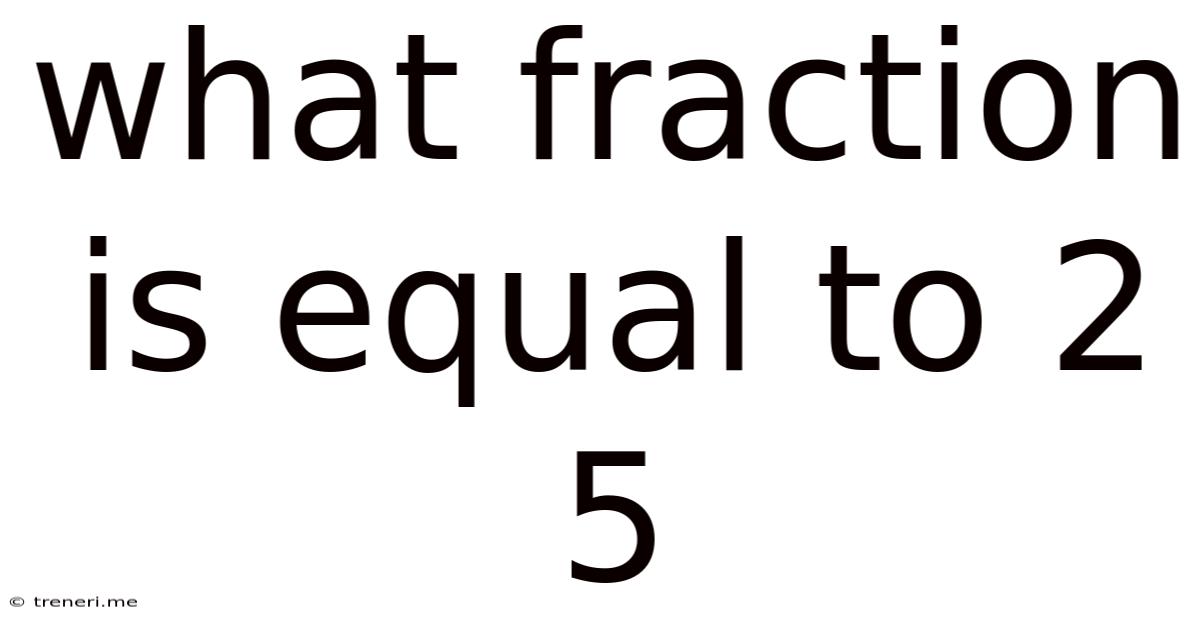
Table of Contents
What Fraction is Equal to 2/5? A Deep Dive into Fractions and Their Equivalents
Understanding fractions is fundamental to mathematics, and mastering the concept of equivalent fractions is crucial for success in various mathematical fields. This comprehensive guide will explore the fraction 2/5, delve into the process of finding equivalent fractions, and discuss various applications and real-world examples. We'll go beyond simply stating the answer and explore the underlying principles, making this a valuable resource for students and anyone looking to refresh their understanding of fractions.
Understanding Fractions: Numerator, Denominator, and the Whole
A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating the number of parts you have. In the fraction 2/5, the numerator is 2.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into. In the fraction 2/5, the denominator is 5.
Therefore, 2/5 represents 2 out of 5 equal parts of a whole.
Finding Equivalent Fractions: The Concept of Multiplication and Division
Equivalent fractions represent the same portion of a whole, even though they look different. We can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. This process doesn't change the value of the fraction; it simply represents the same value in a different form.
For example, let's find some equivalent fractions for 2/5:
- Multiplying by 2: (2 x 2) / (5 x 2) = 4/10
- Multiplying by 3: (2 x 3) / (5 x 3) = 6/15
- Multiplying by 4: (2 x 4) / (5 x 4) = 8/20
- Multiplying by 5: (2 x 5) / (5 x 5) = 10/25
And so on. We can continue this process indefinitely, creating an infinite number of equivalent fractions for 2/5. All these fractions – 2/5, 4/10, 6/15, 8/20, 10/25, etc. – represent the same quantity.
Simplifying Fractions: Finding the Simplest Form
The opposite of finding equivalent fractions by multiplying is simplifying fractions by dividing. Simplifying, or reducing, a fraction means finding its equivalent fraction in its simplest form. This is done by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of two numbers is the largest number that divides both without leaving a remainder. For example, the GCD of 2 and 5 is 1. Since the GCD of 2 and 5 is 1, the fraction 2/5 is already in its simplest form. It cannot be further simplified.
Visual Representation of 2/5 and Its Equivalents
Visualizing fractions can significantly improve understanding. Imagine a rectangular shape divided into 5 equal parts. If we shade 2 of these parts, we visually represent the fraction 2/5.
Now, imagine dividing each of the 5 parts in half. We now have 10 equal parts, and shading 4 of them would represent the equivalent fraction 4/10. Similarly, dividing each of the initial 5 parts into three equal parts would give us 15 smaller parts, and shading 6 of them would represent 6/15, and so on. This visual representation helps to solidify the concept of equivalent fractions.
Applications of 2/5 and Equivalent Fractions in Real Life
Fractions, including 2/5 and its equivalents, are prevalent in various aspects of daily life:
- Cooking and Baking: Recipes often use fractional measurements. If a recipe calls for 2/5 of a cup of sugar, you can use an equivalent fraction like 4/10 or 6/15 of a cup to achieve the same result.
- Measurements: Measuring lengths, weights, or volumes frequently involves fractions. For example, measuring 2/5 of a meter is the same as measuring 4/10 or 6/15 of a meter.
- Sharing and Dividing: When sharing items equally, fractions are essential. If you have 5 cookies and want to share 2/5 of them, you would give away 2 cookies.
- Probability and Statistics: Fractions are used extensively in probability calculations. The probability of an event can be expressed as a fraction.
- Finance and Budgeting: Fractions are vital in finance, representing parts of a whole budget or investment.
Solving Problems Involving 2/5
Let's explore a few example problems involving the fraction 2/5:
Problem 1: A pizza is cut into 5 equal slices. If you eat 2 slices, what fraction of the pizza did you eat?
Solution: You ate 2 out of 5 slices, so you ate 2/5 of the pizza.
Problem 2: A bag contains 10 marbles, 4 of which are red. What fraction of the marbles are red? Is this fraction equivalent to 2/5?
Solution: 4/10 of the marbles are red. Simplifying 4/10 by dividing both the numerator and denominator by 2 gives 2/5. Yes, 4/10 is equivalent to 2/5.
Problem 3: John completed 2/5 of his homework. If his homework has 25 problems, how many problems did he complete?
Solution: We need to find 2/5 of 25. Multiply the numerator (2) by 25 and then divide by the denominator (5): (2 x 25) / 5 = 50/5 = 10. John completed 10 problems.
Beyond the Basics: Decimal and Percentage Equivalents
Fractions can be expressed in other forms, such as decimals and percentages.
- Decimal Equivalent: To convert 2/5 to a decimal, divide the numerator by the denominator: 2 ÷ 5 = 0.4.
- Percentage Equivalent: To convert 2/5 to a percentage, multiply the decimal equivalent by 100: 0.4 x 100 = 40%. Therefore, 2/5 is equal to 40%.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
Understanding fractions, including equivalent fractions and the ability to simplify and convert them to decimals and percentages, is crucial for success in mathematics and various real-world applications. This in-depth exploration of the fraction 2/5 provides a solid foundation for working with fractions and building a stronger mathematical understanding. The examples and explanations provided offer a practical approach to mastering this fundamental concept. Remember that practice is key to solidifying your understanding and building confidence in working with fractions. By consistently applying the principles outlined in this guide, you can confidently tackle more complex mathematical problems involving fractions.
Latest Posts
Latest Posts
-
How Many Cups Is 14 And 1 2 Oz
May 10, 2025
-
Cuantos Dias Faltan Para El Lunes
May 10, 2025
-
Which Side Is Length Of A Rectangle
May 10, 2025
-
How Many Times Does 8 Go Into 20
May 10, 2025
-
How Long Is 42 Months In Years
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.