What Fraction Is Equal To 4/9
Treneri
May 13, 2025 · 6 min read
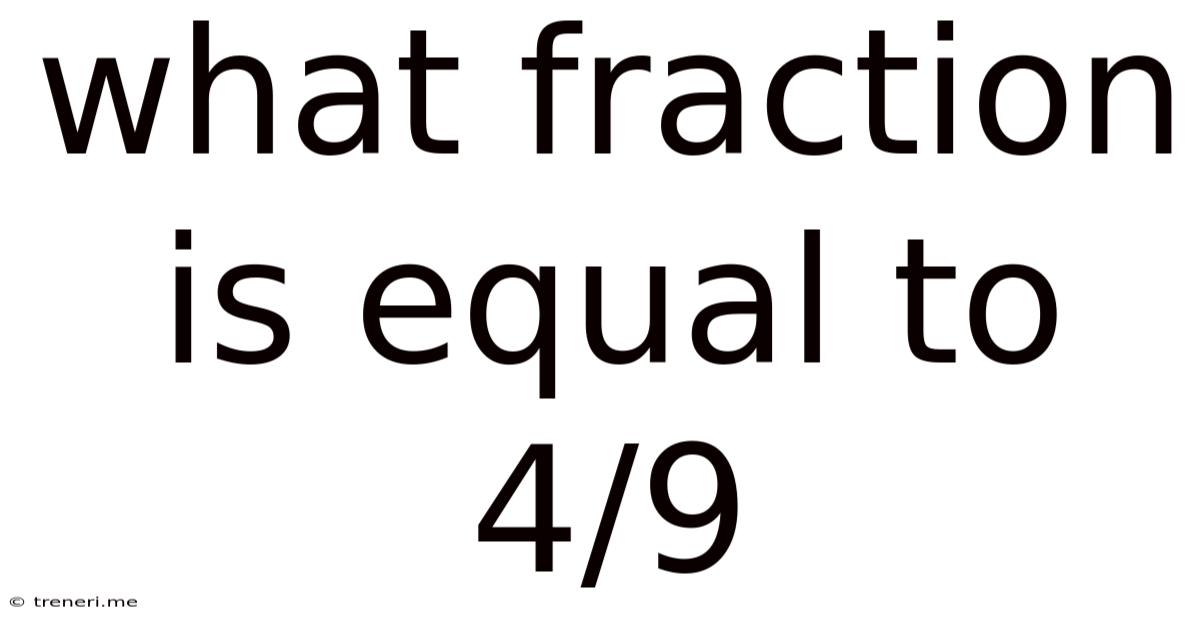
Table of Contents
What Fraction Is Equal to 4/9? Exploring Equivalent Fractions and Their Applications
Understanding fractions is fundamental to mathematics, forming the bedrock for more advanced concepts. This article delves deep into the question, "What fraction is equal to 4/9?", exploring the concept of equivalent fractions, methods for finding them, and practical applications of this knowledge. We'll move beyond simply identifying equivalent fractions to understanding the underlying mathematical principles and how this knowledge can be applied in various real-world scenarios.
Understanding Equivalent Fractions
Equivalent fractions represent the same value, even though they look different. Imagine cutting a pizza into 9 slices. 4/9 represents four out of those nine slices. Now, imagine cutting the same pizza into 18 slices. You would still have the same amount of pizza if you had 8 out of 18 slices (8/18). Both 4/9 and 8/18 represent the same portion of the whole pizza; they are equivalent fractions.
The key to finding equivalent fractions lies in multiplying or dividing both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number. This process doesn't change the fundamental value of the fraction because you are essentially multiplying or dividing by 1 (any number divided by itself equals 1).
Example:
To find an equivalent fraction of 4/9, we can multiply both the numerator and the denominator by 2:
(4 x 2) / (9 x 2) = 8/18
Therefore, 8/18 is an equivalent fraction to 4/9. We could continue this process, multiplying by 3, 4, 5, and so on, to generate an infinite number of equivalent fractions.
Methods for Finding Equivalent Fractions
Several methods can be used to find equivalent fractions, each offering a slightly different approach:
1. Multiplication Method:
This is the most straightforward method. Choose a whole number (greater than 1) and multiply both the numerator and denominator by that number. The resulting fraction will be equivalent to the original.
Example:
Let's find three equivalent fractions for 4/9:
- Multiply by 2: (4 x 2) / (9 x 2) = 8/18
- Multiply by 3: (4 x 3) / (9 x 3) = 12/27
- Multiply by 5: (4 x 5) / (9 x 5) = 20/45
2. Division Method (Simplification):
This method is used to find the simplest equivalent fraction, also known as the fraction in its lowest terms or simplified fraction. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Example:
Let's say we have the fraction 12/27. The GCD of 12 and 27 is 3. Dividing both the numerator and denominator by 3:
12/3 = 4 27/3 = 9
Therefore, the simplified form of 12/27 is 4/9. This demonstrates that 12/27 is an equivalent fraction to 4/9.
3. Using Prime Factorization:
Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). This method is especially useful for finding the simplest form of a fraction and identifying common factors.
Example:
Let's find the simplest form of 20/45 using prime factorization:
- 20 = 2 x 2 x 5
- 45 = 3 x 3 x 5
The common factor is 5. Dividing both numerator and denominator by 5:
20/5 = 4 45/5 = 9
Thus, the simplest form of 20/45 is 4/9.
Applications of Equivalent Fractions
Understanding equivalent fractions isn't just an academic exercise; it has numerous practical applications:
1. Measurement and Conversions:
Equivalent fractions are crucial in converting between different units of measurement. For example, converting inches to feet, ounces to pounds, or centimeters to meters all involve working with equivalent fractions.
2. Recipes and Cooking:
Scaling recipes up or down requires working with equivalent fractions. If a recipe calls for 4/9 of a cup of flour, and you want to double the recipe, you'd need to calculate the equivalent fraction for 8/18 (which simplifies to 4/9) of a cup.
3. Sharing and Division:
Dividing quantities fairly among a group of people often requires using equivalent fractions. If you have 4 pizzas to share among 9 people, each person receives 4/9 of a pizza. If you have 8 pizzas to share amongst 18 people, it's still 4/9 of a pizza each person.
4. Geometry and Area:
Calculations involving areas and shapes frequently use equivalent fractions. Determining the fraction of a shape that's shaded or comparing the areas of similar shapes involves manipulating equivalent fractions.
5. Probability and Statistics:
Probability is often expressed as a fraction. Understanding equivalent fractions allows for simpler representation and comparison of probabilities. For instance, a probability of 4/9 is equivalent to 8/18, 12/27, and so on.
6. Financial Calculations:
In finance, working with fractions and percentages (which are closely related to fractions) is essential. For instance, calculating interest rates, discounts, or profit margins requires a solid understanding of fractions and their equivalents.
7. Data Representation and Analysis:
Representing data using fractions is common in various fields. For example, in surveys or polls, results might be expressed as fractions, and understanding equivalent fractions helps to interpret and compare these results effectively.
Beyond the Basics: More Complex Scenarios
While finding simple equivalent fractions is relatively straightforward, more complex scenarios may require a deeper understanding. For example:
-
Finding a specific equivalent fraction: You might need to find an equivalent fraction with a particular denominator or numerator. This requires solving a proportion. For instance, if you want to find an equivalent fraction of 4/9 with a denominator of 36, you would set up the proportion: 4/9 = x/36. Solving for x gives you x = 16, so the equivalent fraction is 16/36.
-
Comparing fractions: When comparing fractions with different denominators, finding equivalent fractions with a common denominator is essential. This allows for direct comparison of the numerators.
-
Adding and subtracting fractions: Before adding or subtracting fractions, you often need to find equivalent fractions with a common denominator.
Conclusion: Mastering Equivalent Fractions
The question, "What fraction is equal to 4/9?" is deceptively simple. While the answer is an infinite number of fractions (8/18, 12/27, 16/36, and so on), the journey to understanding why this is true, and the myriad ways this knowledge is applied, is far more profound. Mastering the concept of equivalent fractions is crucial not only for academic success but also for navigating many aspects of daily life that rely on fractions, proportions, and the understanding of parts related to a whole. By understanding the methods presented in this article, you can confidently tackle any fraction-related problem and appreciate the power and versatility of this fundamental mathematical concept. This article serves as a comprehensive guide, equipping you with the knowledge and tools to confidently work with equivalent fractions in any context. Remember to practice regularly, and you will develop a strong intuition and mastery over this vital skill.
Latest Posts
Latest Posts
-
Calories Burned 20 Mile Bike Ride
May 14, 2025
-
How To Find 21 Percent Of A Number
May 14, 2025
-
How Many More Days Until The End Of The Month
May 14, 2025
-
How Many Seconds Are In 7 Years
May 14, 2025
-
Cuanto Son 16 Onzas En Mililitros
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 4/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.