What Fraction Is Equal To 5 6
Treneri
May 11, 2025 · 6 min read
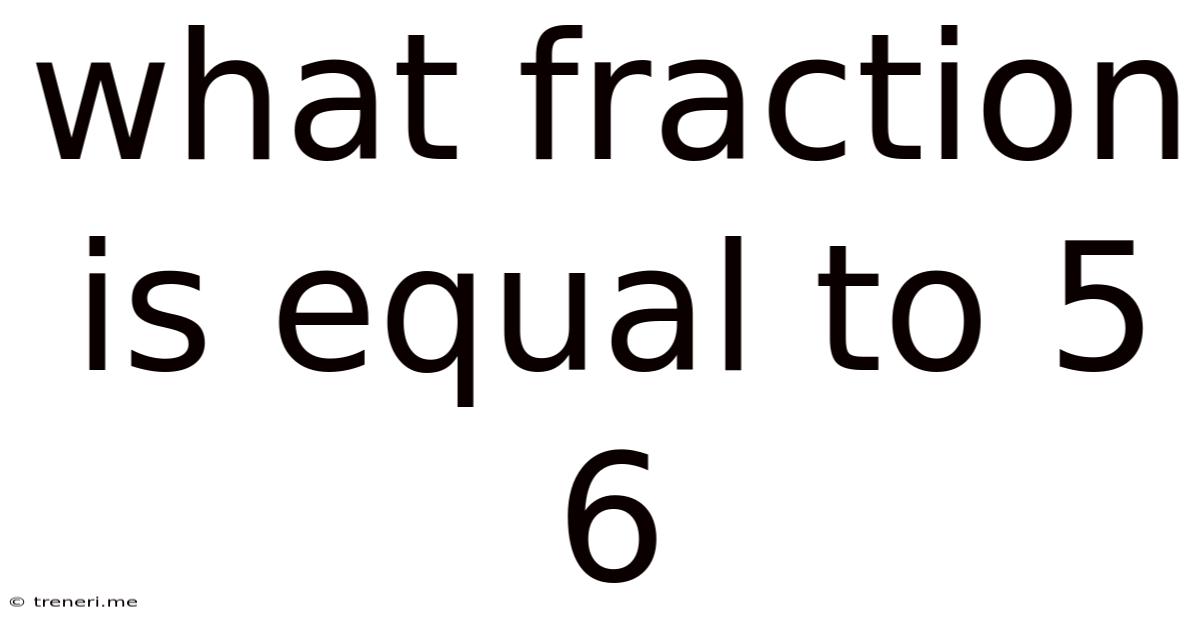
Table of Contents
What Fraction is Equal to 5/6? Exploring Equivalent Fractions and Their Applications
Understanding fractions is fundamental to mathematics and numerous real-world applications. This comprehensive guide delves into the concept of equivalent fractions, specifically focusing on fractions equal to 5/6. We'll explore various methods for finding these equivalent fractions, discuss their practical applications, and offer exercises to solidify your understanding.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion of a whole, even though they appear different. Think of cutting a pizza: one-half (1/2) is the same as two-quarters (2/4), or four-eighths (4/8), etc. They all represent half the pizza. The key is that the ratio between the numerator (top number) and the denominator (bottom number) remains constant.
To find an equivalent fraction, you simply multiply or divide both the numerator and the denominator by the same non-zero number. This is because multiplying or dividing by the same number is essentially multiplying or dividing by 1 (e.g., 2/2 = 1, 3/3 = 1, etc.), which doesn't change the value of the fraction.
Finding Equivalent Fractions for 5/6
Let's find some equivalent fractions for 5/6. We can achieve this by multiplying both the numerator and the denominator by the same whole number.
Examples of Equivalent Fractions:
- Multiply by 2: (5 x 2) / (6 x 2) = 10/12
- Multiply by 3: (5 x 3) / (6 x 3) = 15/18
- Multiply by 4: (5 x 4) / (6 x 4) = 20/24
- Multiply by 5: (5 x 5) / (6 x 5) = 25/30
- Multiply by 10: (5 x 10) / (6 x 10) = 50/60
And so on... You can generate infinitely many equivalent fractions by multiplying by any whole number.
Simplifying Fractions: Finding the Simplest Form
While we can create countless equivalent fractions by multiplying, it's often useful to find the simplest form of a fraction. This is the equivalent fraction where the numerator and denominator have no common factors other than 1 (i.e., they are relatively prime or coprime). This process is called simplification or reducing the fraction.
To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. For instance, let's consider the fraction 10/12.
The factors of 10 are 1, 2, 5, and 10. The factors of 12 are 1, 2, 3, 4, 6, and 12.
The greatest common divisor of 10 and 12 is 2. Dividing both the numerator and the denominator by 2 gives us:
10/2 / 12/2 = 5/6
This confirms that 5/6 is the simplest form of the fraction 10/12 (and many others).
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in various real-world scenarios:
1. Cooking and Baking:
Recipes often require adjusting ingredient quantities. If a recipe calls for 5/6 cup of flour, and you want to double the recipe, you'll need 10/12 cups (or 5/6 x 2 = 10/6 = 5/3 = 1 and 2/3 cups). Understanding equivalent fractions allows for accurate scaling.
2. Measurement:
Measurements often involve fractions (e.g., inches, centimeters, etc.). Converting between different units often requires working with equivalent fractions. For example, converting 5/6 of a foot to inches involves understanding that 1 foot equals 12 inches and then finding the equivalent fraction in inches.
5/6 foot * 12 inches/foot = 60/6 inches = 10 inches
3. Sharing and Division:
When dividing things equally, equivalent fractions come into play. Imagine sharing 5 pizzas amongst 6 people. Each person receives 5/6 of a pizza. If you have 10 pizzas and 12 people, each person still gets the equivalent fraction 10/12 = 5/6 of a pizza.
4. Geometry and Area:
Calculating areas often involves fractions. If a rectangle has a length of 5 units and a width of 6 units, its area is 30 square units. If you have a rectangle of equivalent proportional lengths, say 10 units and 12 units, then its area is 120 square units. This concept demonstrates how the relative size remains consistent despite using different equivalent fractions.
5. Probability and Statistics:
Probability is often expressed as a fraction. If the probability of an event is 5/6, this means that out of 6 possible outcomes, 5 are favorable. Equivalent fractions are useful in comparing and simplifying probabilities. For example, if you roll a die 60 times, the expected number of times a particular event with a probability of 5/6 occurs would be 50 (5/6 x 60).
Working with Mixed Numbers and Improper Fractions
The number 5/6 is a proper fraction (numerator less than the denominator). However, sometimes we deal with improper fractions (numerator greater than or equal to the denominator) or mixed numbers (a whole number and a proper fraction).
Let's consider an example of an improper fraction equivalent to 5/6: There isn't one that's simpler. 5/6 is already in its simplest form. However, you could have, say, 10/12 which simplifies back to 5/6.
To convert an improper fraction into a mixed number, divide the numerator by the denominator. The quotient is the whole number part, and the remainder becomes the numerator of the fractional part. The denominator remains the same.
Converting a mixed number to an improper fraction is the reverse process: Multiply the whole number by the denominator, add the numerator, and place this sum over the denominator.
For example: 1 1/2 = (1*2 + 1)/2 = 3/2. This is an improper fraction.
Understanding this conversion is essential when working with equivalent fractions in more complex problems.
Exercises to Practice
Here are some exercises to help you solidify your understanding:
- Find five equivalent fractions for 5/6.
- Simplify the following fractions: 15/18, 20/24, 30/36, 50/60.
- Convert the improper fraction 17/6 into a mixed number.
- Convert the mixed number 2 1/3 into an improper fraction.
- A recipe calls for 5/6 of a cup of sugar. If you want to make 3 times the recipe, how much sugar do you need? Express your answer as a mixed number.
- If a piece of wood is 5/6 of a meter long, how many centimeters long is it? (Remember 1 meter = 100 centimeters)
Conclusion
Understanding equivalent fractions is a fundamental mathematical skill with widespread applications. By mastering the techniques of finding, simplifying, and converting between different fraction forms, you equip yourself with the tools to tackle numerous mathematical and real-world challenges. Remember, the key is to always maintain the ratio between the numerator and denominator while manipulating the numbers. Through practice and consistent application, you will confidently navigate the world of fractions and their endless possibilities.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 39 And 6
May 11, 2025
-
10 Dollars A Second For A Day
May 11, 2025
-
How To Find The Range Of A Projectile
May 11, 2025
-
196 Km To Miles Per Hour
May 11, 2025
-
How Many Calories Does 1 G Of Protein Have
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.