What Fraction Is Equivalent To 3/9
Treneri
May 12, 2025 · 5 min read
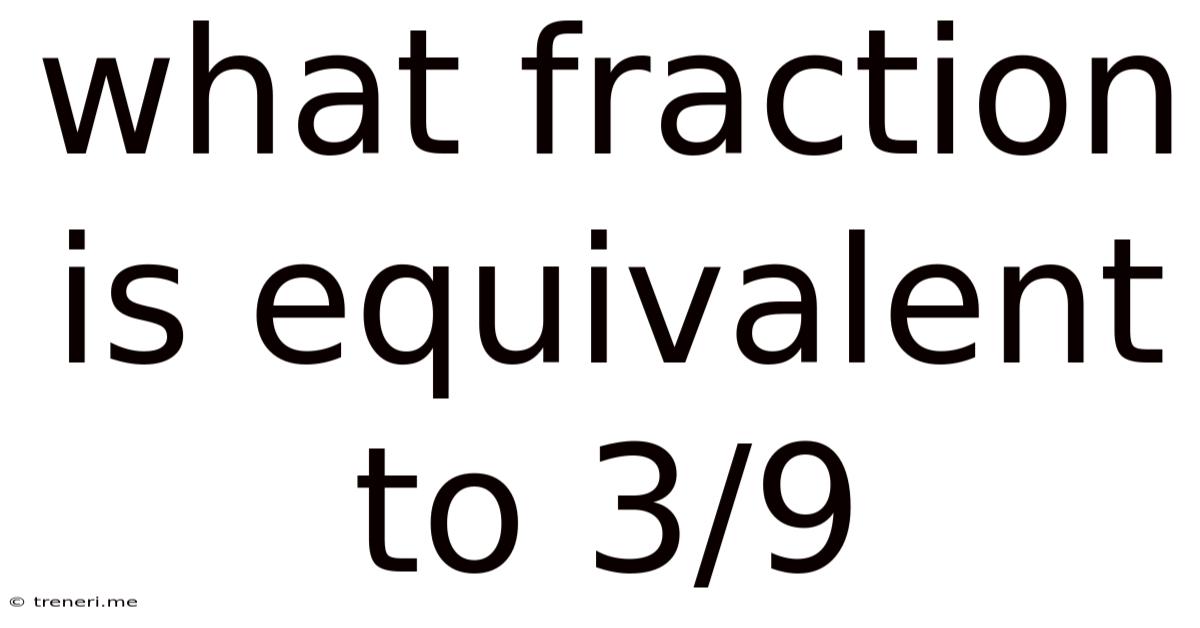
Table of Contents
What Fraction Is Equivalent to 3/9? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially when dealing with straightforward examples like 3/9. However, understanding the underlying principles and exploring various methods to solve such problems is crucial for building a strong foundation in mathematics. This comprehensive guide will not only answer the question "What fraction is equivalent to 3/9?" but will also delve into the broader concept of equivalent fractions, exploring different approaches and providing practical examples.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear differently. Imagine cutting a pizza into 9 slices and taking 3. This is represented by the fraction 3/9. Now, imagine cutting the same pizza into fewer slices, say 3, and taking only 1 slice. You've still consumed the same amount of pizza. This smaller portion is represented by the fraction 1/3. Both 3/9 and 1/3 represent the same value – one-third of the pizza.
Key Principle: Equivalent fractions are created by multiplying or dividing both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number. This process maintains the ratio between the numerator and the denominator, ensuring the fractional value remains constant.
Finding the Equivalent Fraction of 3/9
The simplest way to find an equivalent fraction for 3/9 is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator (3) and the denominator (9) and dividing both by it.
1. Finding the Greatest Common Divisor (GCD)
The GCD of 3 and 9 is 3. This means 3 is the largest number that divides both 3 and 9 without leaving a remainder.
2. Simplifying the Fraction
Dividing both the numerator and the denominator of 3/9 by the GCD (3), we get:
3 ÷ 3 / 9 ÷ 3 = 1/3
Therefore, the simplest equivalent fraction of 3/9 is 1/3.
Other Equivalent Fractions
While 1/3 is the simplest form, there are infinitely many other fractions equivalent to 3/9. We can obtain these by multiplying both the numerator and the denominator by the same number.
Let's demonstrate this:
- Multiplying by 2: (3 x 2) / (9 x 2) = 6/18
- Multiplying by 3: (3 x 3) / (9 x 3) = 9/27
- Multiplying by 4: (3 x 4) / (9 x 4) = 12/36
- Multiplying by 5: (3 x 5) / (9 x 5) = 15/45
And so on... All these fractions – 6/18, 9/27, 12/36, 15/45, and countless others – are equivalent to 3/9 and 1/3.
Visual Representation of Equivalent Fractions
Visual aids can greatly enhance understanding. Imagine a rectangle divided into 9 equal parts. Shading 3 of these parts visually represents the fraction 3/9. Now, consider a smaller rectangle divided into only 3 equal parts. Shading one part represents 1/3. Both shaded areas visually demonstrate that 3/9 and 1/3 represent the same proportion. This visual comparison reinforces the concept of equivalence.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is not just an abstract mathematical concept; it has numerous real-world applications:
-
Cooking and Baking: Recipes often require adjusting ingredient quantities. If a recipe calls for 3/9 cup of sugar and you want to halve the recipe, you'd need to find an equivalent fraction of 3/9 that is easily divisible by 2 (like 1/3 cup).
-
Measurement and Conversions: Converting between different units of measurement often involves working with equivalent fractions. For example, converting inches to feet requires understanding that 12 inches are equivalent to 1 foot.
-
Data Analysis and Statistics: Representing data as fractions often involves simplifying fractions to their lowest terms for easier interpretation and comparison.
-
Geometry and Area Calculations: Calculating areas of shapes often involves using fractions, and simplifying these fractions makes calculations simpler.
Methods for Determining Equivalent Fractions
Beyond simply finding the GCD, several methods can be used to determine if two fractions are equivalent:
1. Cross-Multiplication: This method involves multiplying the numerator of one fraction by the denominator of the other and vice-versa. If the products are equal, the fractions are equivalent.
For example, let's check if 3/9 and 1/3 are equivalent:
(3 x 3) = 9 (9 x 1) = 9
Since both products are equal, 3/9 and 1/3 are indeed equivalent.
2. Finding a Common Denominator: This method involves converting both fractions to have the same denominator. If the numerators are also equal after this conversion, the fractions are equivalent.
Let's compare 3/9 and 1/3 using this method:
To get a common denominator, we can multiply the numerator and denominator of 1/3 by 3:
(1 x 3) / (3 x 3) = 3/9
Since both fractions are now 3/9, they are equivalent.
Advanced Concepts Related to Equivalent Fractions
Exploring equivalent fractions opens doors to more advanced mathematical concepts:
-
Ratios and Proportions: Equivalent fractions are fundamentally related to ratios and proportions. A ratio expresses the relationship between two quantities, and equivalent fractions represent equivalent ratios.
-
Decimal Representation: Every fraction can be expressed as a decimal, and equivalent fractions will have the same decimal representation. For example, 3/9 and 1/3 both equal 0.333... (a repeating decimal).
-
Percentage Representation: Fractions can be converted to percentages, and equivalent fractions will represent the same percentage. 3/9 and 1/3 both represent 33.33...%
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is a fundamental skill in mathematics with broad applications. This guide has explored various methods for identifying equivalent fractions, emphasizing the importance of simplifying to the lowest terms and using visual representations for clarity. Mastering this concept forms a strong foundation for tackling more complex mathematical problems and real-world applications. Remember, the key is to understand the underlying principle: multiplying or dividing both the numerator and denominator by the same non-zero number preserves the fraction's value, creating an equivalent representation. By applying these methods and concepts, you'll confidently navigate the world of fractions and their diverse applications.
Latest Posts
Latest Posts
-
86 Grams Is How Many Ounces
May 14, 2025
-
What Is The Slope Of The Equation Mc016 1 Jpg
May 14, 2025
-
Cuantos Bloques Lleva Una Pared De 4 Metros
May 14, 2025
-
What Is 10 Ml In Oz
May 14, 2025
-
11 Ounces Equals How Many Cups
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equivalent To 3/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.