What Fraction Is Equivalent To 5/6
Treneri
May 12, 2025 · 6 min read
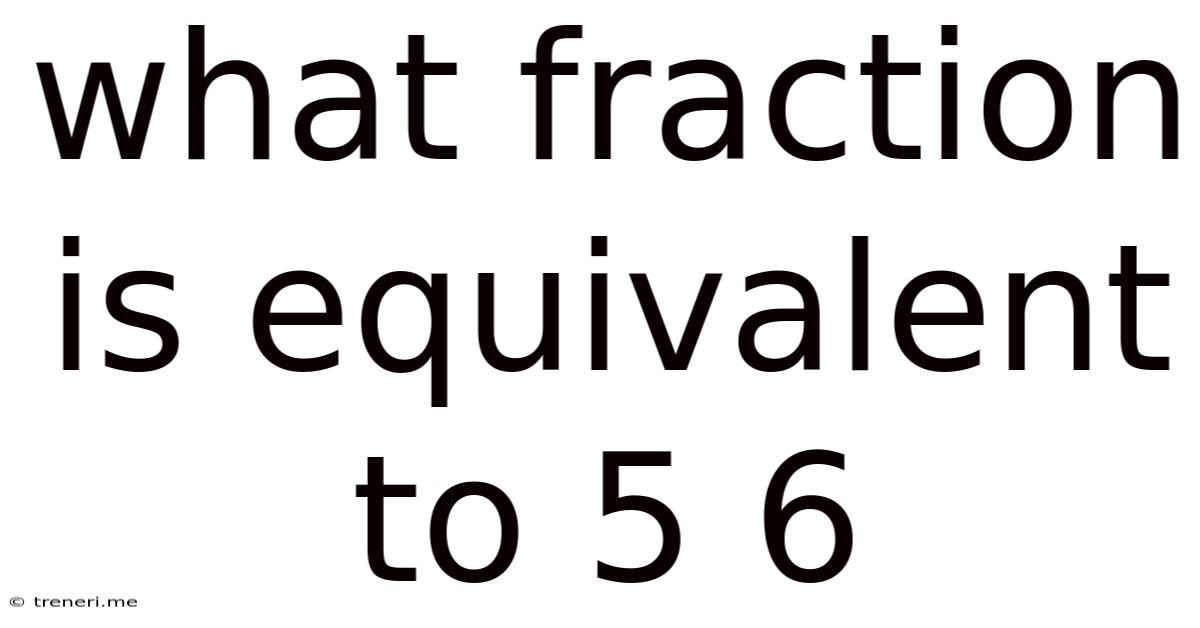
Table of Contents
What Fraction is Equivalent to 5/6? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially when dealing with straightforward fractions like 5/6. However, understanding the underlying principles of equivalent fractions is crucial for mastering more complex mathematical concepts. This comprehensive guide delves into the concept of equivalent fractions, focusing on 5/6 and exploring various methods to determine its equivalents. We'll also touch upon practical applications and why understanding this concept is vital in various fields.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. Imagine slicing a pizza: one half (1/2) is the same as two quarters (2/4), or four eighths (4/8). These are all equivalent fractions. The key principle is that the ratio between the numerator (top number) and the denominator (bottom number) remains constant.
To find an equivalent fraction, you multiply or divide both the numerator and the denominator by the same non-zero number. This ensures that the ratio remains unchanged, maintaining the same value.
Methods for Finding Equivalent Fractions of 5/6
Let's explore several ways to find equivalent fractions of 5/6:
1. Multiplying the Numerator and Denominator
The simplest method is to multiply both the numerator and denominator by the same whole number. For example:
- Multiply by 2: (5 x 2) / (6 x 2) = 10/12
- Multiply by 3: (5 x 3) / (6 x 3) = 15/18
- Multiply by 4: (5 x 4) / (6 x 4) = 20/24
- Multiply by 5: (5 x 5) / (6 x 5) = 25/30
- Multiply by 10: (5 x 10) / (6 x 10) = 50/60
And so on. You can continue this process indefinitely, generating an infinite number of equivalent fractions for 5/6. Each resulting fraction represents the same proportion of a whole.
2. Using a Common Factor
Alternatively, you can start with a larger fraction and simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, let's consider the fraction 30/36:
- Find the GCD of 30 and 36: The GCD of 30 and 36 is 6.
- Divide both the numerator and denominator by the GCD: 30 ÷ 6 = 5 and 36 ÷ 6 = 6.
- Result: The simplified fraction is 5/6. Therefore, 30/36 is an equivalent fraction to 5/6.
This method works in reverse as well. If you start with 5/6 and multiply both by a number, you can then find the GCD to simplify and end up back at 5/6. This reinforces the concept of equivalence.
3. Visual Representation
A visual approach can aid understanding. Imagine a rectangular shape divided into six equal parts. Shading five of these parts represents the fraction 5/6. Now imagine dividing each of those six parts into two smaller parts. You'll now have twelve smaller parts, and ten of them will be shaded, giving you the equivalent fraction 10/12. This visual representation clearly shows that 5/6 and 10/12 represent the same area.
Why Understanding Equivalent Fractions Matters
The ability to identify and work with equivalent fractions is essential in various mathematical contexts and real-world applications:
1. Simplifying Fractions
Reducing fractions to their simplest form (lowest terms) makes them easier to understand and work with. This simplifies calculations and avoids unnecessarily large numbers. For instance, 10/12 is less intuitive than its simplified equivalent, 5/6.
2. Comparing Fractions
When comparing fractions, it's often necessary to find equivalent fractions with a common denominator. This allows for direct comparison of the numerators. For example, comparing 5/6 and 2/3 requires finding a common denominator (6), making the comparison between 5/6 and 4/6 straightforward.
3. Adding and Subtracting Fractions
Adding or subtracting fractions requires a common denominator. Finding equivalent fractions with a common denominator is a crucial step in these operations. For example, to add 5/6 and 1/3, we would find an equivalent fraction for 1/3 (which is 2/6), then add 5/6 + 2/6 = 7/6.
4. Real-World Applications
Equivalent fractions pop up in countless real-world situations:
- Cooking: A recipe might call for 1/2 cup of sugar, which is equivalent to 2/4 cup, or 4/8 cup, allowing for flexibility in measurements.
- Construction: Measuring materials accurately often involves converting between fractions and decimals, relying on the understanding of equivalent fractions.
- Data Analysis: Representing proportions and percentages frequently involves working with fractions and their equivalents.
Beyond the Basics: Infinite Equivalents and Decimal Representation
It's crucial to understand that there are infinitely many equivalent fractions for any given fraction. This is because you can always multiply the numerator and denominator by any non-zero whole number.
Furthermore, every fraction can be expressed as a decimal. To find the decimal equivalent of 5/6, you simply divide the numerator (5) by the denominator (6): 5 ÷ 6 = 0.8333... (a repeating decimal). This decimal representation offers another way to demonstrate the equivalence of fractions; all equivalent fractions will have the same decimal representation (or a closely related one accounting for rounding).
Advanced Concepts and Problem Solving
Let's consider a more complex scenario to showcase the application of equivalent fractions:
Problem: A carpenter needs to cut a board that is 5/6 of a meter long. They only have a measuring tape marked in centimeters (1 meter = 100 centimeters). How many centimeters should they cut?
Solution:
- Convert the fraction to centimeters: Since 1 meter = 100 centimeters, 5/6 of a meter is (5/6) * 100 centimeters.
- Simplify the expression: (5 * 100) / 6 = 500/6 centimeters.
- Simplify the fraction: 500/6 simplifies to 250/3 centimeters.
- Convert to a mixed number or decimal: 250/3 is approximately 83.33 centimeters.
This problem highlights the practicality of understanding equivalent fractions in real-world applications. The ability to convert between different units and work with fractions is essential for precise measurements.
Conclusion
Understanding equivalent fractions is fundamental to mastering various mathematical concepts. While finding equivalent fractions for 5/6 might seem straightforward initially, grasping the underlying principles allows for the successful manipulation of fractions in more complex scenarios. By mastering the techniques and recognizing the importance of equivalent fractions across various applications, you build a stronger foundation in mathematics and problem-solving skills applicable to numerous fields. Remember that practice is key—the more you work with equivalent fractions, the more intuitive the process becomes. From simple arithmetic to complex engineering calculations, the ability to effortlessly work with equivalent fractions remains invaluable.
Latest Posts
Latest Posts
-
30 Rounded To The Nearest Ten
May 12, 2025
-
Volume Water Tank Capacity Calculation Formula Pdf
May 12, 2025
-
25 Libras En Kilos Cuanto Es
May 12, 2025
-
Common Denominator Of 8 And 3
May 12, 2025
-
100 Is 1 10 Of What Number
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equivalent To 5/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.