What Fraction Is Equivalent To 6/8
Treneri
May 09, 2025 · 6 min read
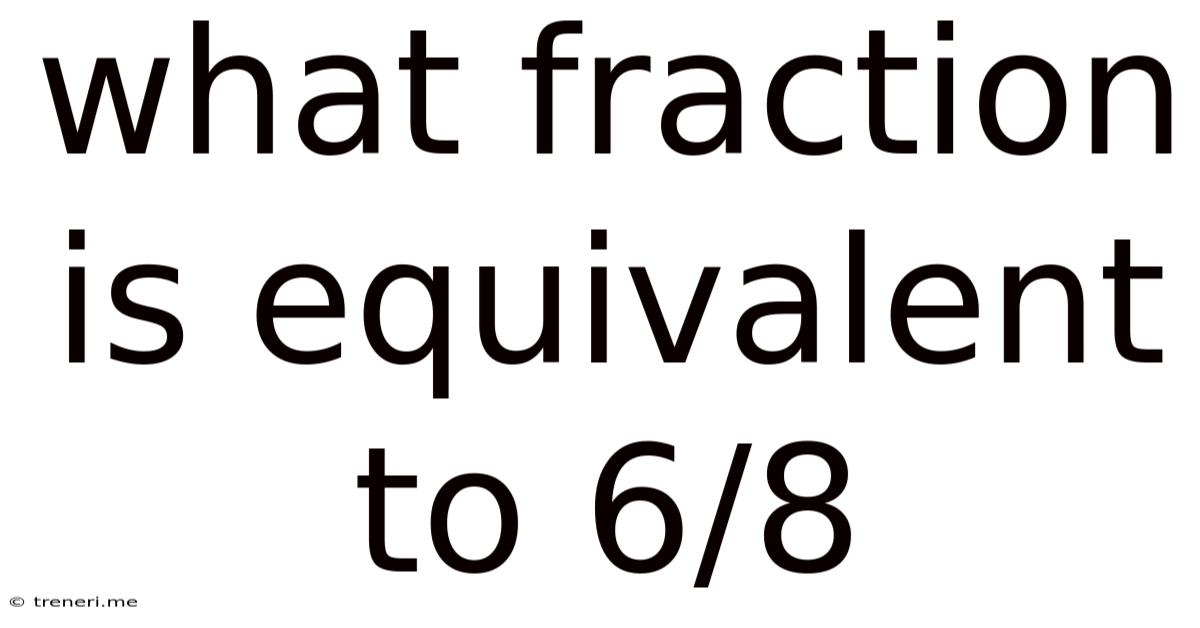
Table of Contents
What Fraction Is Equivalent to 6/8? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially for younger learners. However, understanding the underlying principles of equivalent fractions is crucial for mastering more complex mathematical concepts later on. This comprehensive guide will explore the concept of equivalent fractions, focusing specifically on fractions equivalent to 6/8, while delving into the broader applications and importance of this fundamental mathematical skill.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value of a whole, even though they appear different. Think of it like having a pizza: you can cut it into 8 slices and eat 6, or you can cut it into 4 slices and eat 3 – you've consumed the same amount of pizza in both instances. The fractions 6/8 and 3/4 represent these equivalent portions.
The key to finding equivalent fractions lies in the principle of multiplying or dividing both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number. This process maintains the ratio between the numerator and the denominator, thus preserving the value of the fraction.
Example:
- Multiplying both the numerator and denominator of 1/2 by 2 gives us 2/4. Both 1/2 and 2/4 represent one-half.
- Dividing both the numerator and denominator of 6/8 by 2 gives us 3/4. Both 6/8 and 3/4 represent the same portion.
This process of multiplying or dividing by the same number is often referred to as simplifying fractions or finding the simplest form.
Finding Fractions Equivalent to 6/8
The fraction 6/8 represents six-eighths of a whole. To find equivalent fractions, we need to find numbers that we can multiply or divide both 6 and 8 by. Let's explore various methods and examples:
Method 1: Dividing by the Greatest Common Factor (GCF)
The most efficient way to find the simplest form of a fraction is to divide both the numerator and the denominator by their greatest common factor (GCF). The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder.
In the case of 6/8, the factors of 6 are 1, 2, 3, and 6, while the factors of 8 are 1, 2, 4, and 8. The greatest common factor of 6 and 8 is 2.
Therefore, we divide both the numerator and denominator by 2:
6 ÷ 2 = 3 8 ÷ 2 = 4
This gives us the simplest form of 6/8, which is 3/4.
Method 2: Multiplying by a Common Factor
Instead of simplifying, we can also create equivalent fractions by multiplying both the numerator and the denominator by the same number. This expands the fraction to a larger, but equivalent, representation.
Let's multiply both the numerator and the denominator of 6/8 by 2:
6 × 2 = 12 8 × 2 = 16
This gives us the equivalent fraction 12/16.
Let's try multiplying by 3:
6 × 3 = 18 8 × 3 = 24
This gives us another equivalent fraction: 18/24.
We can continue this process, multiplying by any whole number, to generate an infinite number of equivalent fractions.
Method 3: Using Visual Representations
Visual representations are excellent for understanding the concept of equivalent fractions, especially for younger learners. Imagine a circle divided into eight equal parts, where six parts are shaded. This visually represents 6/8. Now, imagine dividing that same circle into four equal parts instead; three of those parts would correspond to the six shaded sections from the previous representation, showing the equivalence between 6/8 and 3/4.
Similarly, you can use other shapes like rectangles or bars to visually represent the fractions and their equivalence.
Applications of Equivalent Fractions
Understanding equivalent fractions is not merely an academic exercise; it's a fundamental skill with wide-ranging applications in various fields, including:
-
Baking and Cooking: Recipes often require adjusting ingredient quantities. Knowing how to find equivalent fractions allows you to easily scale recipes up or down while maintaining the correct proportions. For example, if a recipe calls for 1/2 cup of sugar and you need to double the recipe, you know that 1/2 is equivalent to 2/4, and thus you would use 2/4 or 1 cup of sugar.
-
Measurement and Conversions: Equivalent fractions are essential when converting units of measurement. Converting between inches and feet, centimeters and meters, or ounces and pounds often involves working with fractions and requires understanding equivalent values.
-
Geometry and Area Calculations: Calculating areas of shapes often involves fractions. Understanding equivalent fractions helps in simplifying calculations and comparing different areas.
-
Data Analysis and Statistics: Representing data in fractions often necessitates finding equivalent fractions to simplify the data and make it easier to interpret.
-
Algebra and Higher Mathematics: Equivalent fractions form the foundation for many concepts in algebra and higher-level mathematics, including solving equations, simplifying expressions, and working with ratios and proportions.
Beyond 6/8: Mastering the Concept of Equivalent Fractions
The principles applied to finding fractions equivalent to 6/8 can be applied to any fraction. The key is always to remember the core principle: multiplying or dividing both the numerator and the denominator by the same non-zero number.
To reinforce this concept, practice with various fractions. Start with simple fractions and gradually progress to more complex ones. Use visual aids, such as diagrams or fraction bars, to solidify your understanding. Regular practice will build confidence and mastery of this essential skill.
Troubleshooting Common Mistakes
Students often make mistakes when working with equivalent fractions. Here are some common errors and how to avoid them:
-
Only multiplying or dividing the numerator or denominator: Remember, you must perform the same operation (multiplication or division) on both the numerator and the denominator. Only changing one will alter the value of the fraction.
-
Incorrectly finding the GCF: When simplifying fractions, ensure you correctly identify the greatest common factor. Practice finding the GCF of different number pairs to improve accuracy.
-
Not simplifying completely: Always check if the simplified fraction can be reduced further. Continue dividing by the GCF until you reach the simplest form.
Conclusion: The Importance of Equivalent Fractions
Mastering equivalent fractions is a cornerstone of mathematical proficiency. Its applications extend far beyond the classroom, impacting everyday life and becoming crucial in various fields. By understanding the underlying principles, practicing regularly, and avoiding common mistakes, you can confidently navigate the world of fractions and unlock a deeper understanding of mathematical concepts. The seemingly simple task of finding a fraction equivalent to 6/8 opens the door to a wider comprehension of mathematical relationships and their practical applications in various aspects of life. Consistent practice and a focus on understanding the underlying principles will solidify your understanding and pave the way for success in more advanced mathematical concepts.
Latest Posts
Latest Posts
-
1 Cm Cube Is Equal To How Many Litres
May 10, 2025
-
Difference Between Ml And Mg In Medicine
May 10, 2025
-
Cuanto Es 20 Oz En Mililitros
May 10, 2025
-
How To Convert From Slope Intercept Form To Standard Form
May 10, 2025
-
How To Find Magnitude Of Frictional Force
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equivalent To 6/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.