What Fraction Is Equivalent To 8/10
Treneri
May 10, 2025 · 5 min read
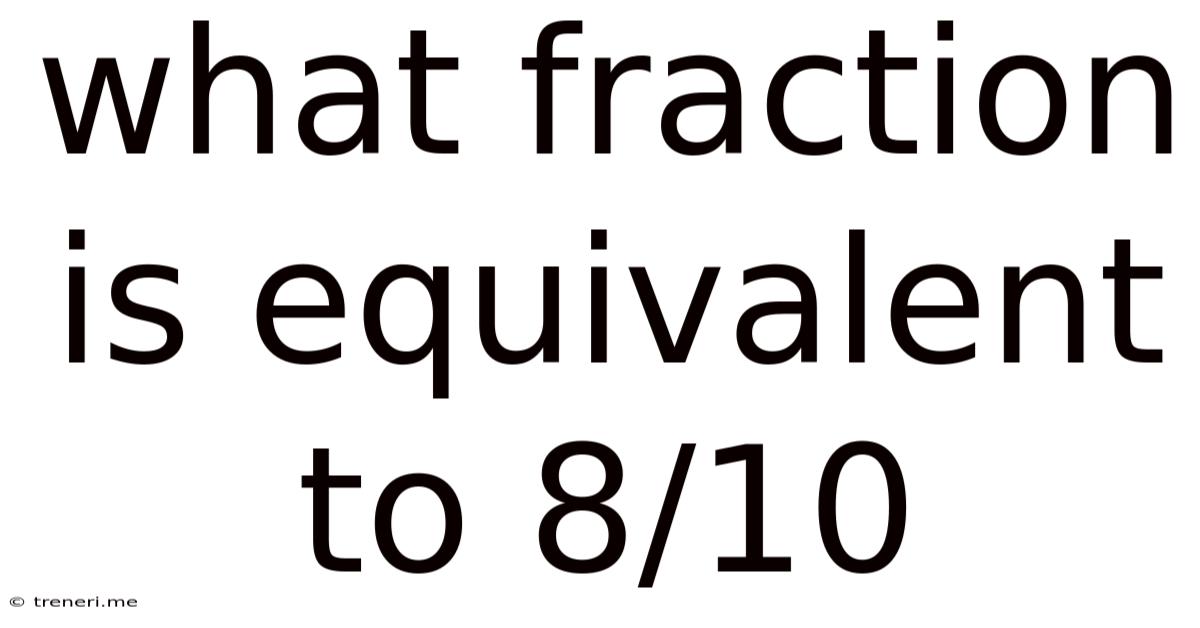
Table of Contents
What Fraction Is Equivalent to 8/10? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially with a straightforward fraction like 8/10. However, understanding the underlying principles and exploring various methods to solve this and similar problems is crucial for building a strong foundation in mathematics. This comprehensive guide will delve into the concept of equivalent fractions, explain how to find them, and provide numerous examples and practical applications. We will also explore the connection between equivalent fractions and simplifying fractions to their lowest terms.
Understanding Equivalent Fractions
Equivalent fractions represent the same value, even though they look different. Think of it like having a pizza. If you cut the pizza into 10 slices and take 8, you've eaten 8/10 of the pizza. If you cut the same pizza into 5 slices (by combining smaller slices), and you take 4, you've still eaten the same amount – 4/5 of the pizza. Therefore, 8/10 and 4/5 are equivalent fractions.
The key to understanding equivalent fractions lies in the concept of multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number. This process doesn't change the overall value of the fraction; it simply changes its representation.
The Fundamental Principle of Equivalent Fractions
The fundamental principle underpinning equivalent fractions is this: Multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number results in an equivalent fraction.
Let's illustrate this with 8/10:
-
Dividing by 2: If we divide both 8 and 10 by 2, we get 4/5. Therefore, 8/10 = 4/5.
-
Multiplying by any number: We can multiply both the numerator and the denominator by any non-zero number (e.g., 3, 5, 100) to find other equivalent fractions:
- Multiplying by 3: (8 x 3) / (10 x 3) = 24/30
- Multiplying by 5: (8 x 5) / (10 x 5) = 40/50
- Multiplying by 100: (8 x 100) / (10 x 100) = 800/1000
All these fractions – 24/30, 40/50, 800/1000 – are equivalent to 8/10 and 4/5.
Finding Equivalent Fractions: Step-by-Step Guide
Here's a step-by-step process for finding equivalent fractions:
-
Identify the given fraction: In our case, it's 8/10.
-
Choose a common factor: Determine a number that divides both the numerator and the denominator without leaving a remainder. For 8/10, a common factor is 2.
-
Divide both the numerator and denominator by the chosen factor: Divide 8 by 2 and 10 by 2. This gives you 4/5.
-
Verify: Check if the resulting fraction is in its simplest form (i.e., the greatest common divisor (GCD) of the numerator and denominator is 1). 4 and 5 have no common factors other than 1, so 4/5 is the simplest form.
-
Generate more equivalent fractions (optional): Multiply both the numerator and denominator by any non-zero integer to create more equivalent fractions. For example, multiplying 4/5 by 3 gives 12/15.
Simplifying Fractions to Lowest Terms
Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This is also known as finding the lowest terms or simplest form of a fraction.
To simplify 8/10, we need to find the greatest common divisor (GCD) of 8 and 10. The GCD of 8 and 10 is 2. Dividing both the numerator and denominator by 2 gives us 4/5, which is the simplest form of 8/10.
Methods for Finding the Greatest Common Divisor (GCD)
Several methods exist for finding the GCD of two numbers:
-
Listing Factors: List all the factors of both numbers and identify the largest common factor.
-
Prime Factorization: Express both numbers as a product of prime numbers. The GCD is the product of the common prime factors raised to the lowest power. For example:
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
- The common prime factor is 2, and the lowest power is 2¹, so the GCD is 2.
-
Euclidean Algorithm: This is an efficient algorithm for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Real-World Applications of Equivalent Fractions
Understanding equivalent fractions is essential in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require adjusting ingredient amounts. If a recipe calls for 2/3 cup of sugar, and you want to double the recipe, you need to find an equivalent fraction for 4/6 (or simply 2/3 * 2 = 4/3).
-
Measurement: Converting between different units of measurement often involves working with equivalent fractions. For example, converting inches to feet or centimeters to meters.
-
Finance: Calculating percentages, interest rates, and proportions in financial calculations relies heavily on the concept of equivalent fractions.
-
Construction and Engineering: Precise measurements and scaling in blueprints and designs depend on the ability to work with equivalent fractions.
Beyond 8/10: Practice Problems
Let's practice finding equivalent fractions with some other examples:
-
Find three equivalent fractions for 3/4:
- Multiplying by 2: 6/8
- Multiplying by 3: 9/12
- Multiplying by 4: 12/16
-
Simplify 12/18 to its lowest terms: The GCD of 12 and 18 is 6. Dividing both by 6 gives 2/3.
-
Determine if 15/20 and 3/4 are equivalent: Simplify 15/20 (GCD is 5) to 3/4. Since both fractions simplify to 3/4, they are equivalent.
-
Find an equivalent fraction for 5/7 with a denominator of 21: We need to multiply the denominator (7) by 3 to get 21. Therefore, we multiply both the numerator and denominator by 3: (5 x 3) / (7 x 3) = 15/21
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is a fundamental skill in mathematics with wide-ranging applications. By mastering the techniques outlined in this guide – including finding the greatest common divisor, simplifying fractions to their lowest terms, and generating equivalent fractions through multiplication and division – you will build a strong foundation for tackling more advanced mathematical concepts. Remember, practice is key! The more you work with equivalent fractions, the more intuitive and comfortable you will become with this crucial mathematical tool. Consistent practice and a solid understanding of the underlying principles will ensure your success in various mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 7 12 As A Grade
May 11, 2025
-
How To Calculate The Slope Of A Ramp
May 11, 2025
-
How Far Is 13 000 Steps
May 11, 2025
-
5 Pounds Of Mashed Potatoes Feeds How Many
May 11, 2025
-
Find The Perimeter Of Quadrilateral Abcd
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equivalent To 8/10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.