What Fractions Are Equal To 2/5
Treneri
May 09, 2025 · 5 min read
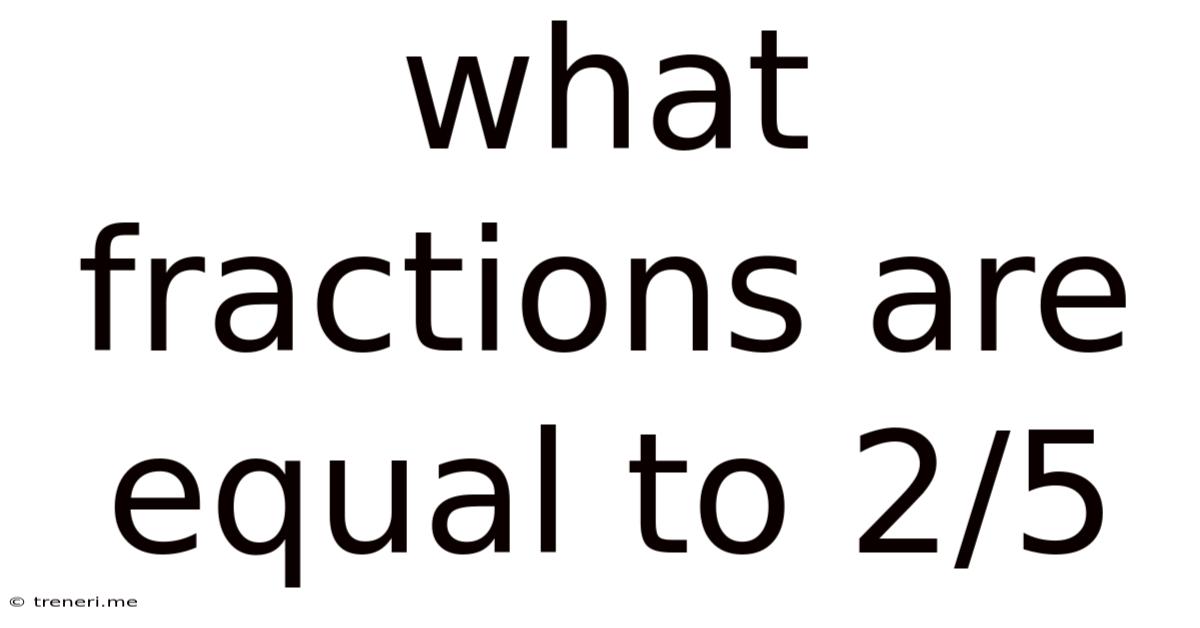
Table of Contents
What Fractions Are Equal to 2/5? A Comprehensive Guide
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding ratios, proportions, and various arithmetic operations. This comprehensive guide delves deep into the question: What fractions are equal to 2/5? We'll explore multiple methods to identify these equivalent fractions, discuss their practical applications, and address common misconceptions.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. They are essentially different ways of expressing the same ratio. The key to understanding equivalent fractions lies in the concept of multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number. This process maintains the original ratio, thus creating an equivalent fraction.
For example, if we multiply both the numerator and denominator of 2/5 by 2, we get 4/10. Both 2/5 and 4/10 represent the same portion – two-fifths. Similarly, multiplying by 3 gives us 6/15, by 4 gives 8/20, and so on. Dividing would also work in reverse; dividing both by 2 would get us 1/2.5, which is less preferable as it contains a decimal. The key is that any fraction formed by multiplying or dividing both the numerator and denominator by the same number (except 0) will be equivalent to the original fraction.
Methods for Finding Equivalent Fractions of 2/5
There are several ways to determine fractions equivalent to 2/5:
1. Multiplying the Numerator and Denominator
This is the most straightforward method. Choose any whole number (other than zero) and multiply both the numerator (2) and the denominator (5) by that number. This will generate an equivalent fraction. Let's illustrate with a few examples:
- Multiply by 2: (2 x 2) / (5 x 2) = 4/10
- Multiply by 3: (2 x 3) / (5 x 3) = 6/15
- Multiply by 4: (2 x 4) / (5 x 4) = 8/20
- Multiply by 5: (2 x 5) / (5 x 5) = 10/25
- Multiply by 10: (2 x 10) / (5 x 10) = 20/50
- Multiply by 100: (2 x 100) / (5 x 100) = 200/500
This process can be repeated indefinitely, generating an infinite number of equivalent fractions.
2. Simplifying Fractions to 2/5
Sometimes you might encounter a fraction that appears different but is actually equivalent to 2/5. In these cases, you need to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example:
Let's consider the fraction 20/50. The GCD of 20 and 50 is 10. Dividing both the numerator and denominator by 10 gives us:
20/10 / 50/10 = 2/5
Therefore, 20/50 is equivalent to 2/5. This method is particularly useful when dealing with larger numbers.
3. Using the Concept of Ratios
Remember that a fraction represents a ratio. 2/5 can be read as "2 out of 5". Any other ratio that maintains this proportion will be an equivalent fraction. For example, if you have 4 parts out of 10 total parts, this is the same ratio as 2 out of 5. Understanding ratios helps intuitively recognize equivalent fractions.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is not just a theoretical exercise; it has numerous practical applications in various fields:
- Cooking and Baking: Recipe scaling often requires converting fractions. If a recipe calls for 2/5 cup of sugar, you might need to find an equivalent fraction using a different measuring cup.
- Construction and Engineering: Precise measurements are vital, and equivalent fractions are used to convert between different units or to simplify calculations.
- Finance: Working with percentages often involves converting fractions to decimals and vice-versa. Understanding equivalent fractions simplifies these conversions.
- Data Analysis: Representing data proportions visually (like in pie charts) may necessitate finding equivalent fractions to simplify the presentation.
- Everyday Life: Dividing items fairly among people often involves using equivalent fractions to ensure equitable distribution.
Common Misconceptions About Equivalent Fractions
Some common misunderstandings related to equivalent fractions include:
- Adding or Subtracting the Same Number: A common mistake is adding or subtracting the same number to both the numerator and denominator. This does not produce an equivalent fraction. Only multiplication and division by the same non-zero number maintain equivalence.
- Ignoring Simplification: Failing to simplify fractions to their lowest terms can lead to unnecessary complexity in calculations and comparisons.
- Confusing Equivalent Fractions with Equal Fractions: Equivalent fractions are equal in value, but the numbers used are different. It's important to distinguish between the concept of equivalence and numerical equality.
Advanced Considerations: Decimal Equivalents and Percentages
The fraction 2/5 can also be expressed as a decimal and a percentage. To find the decimal equivalent, simply divide the numerator by the denominator:
2 ÷ 5 = 0.4
To express this as a percentage, multiply the decimal by 100:
0.4 x 100 = 40%
Therefore, 2/5 is equivalent to 0.4 and 40%. This highlights the interconnectedness of different numerical representations. Understanding these conversions helps in solving problems across various mathematical contexts.
Conclusion: Mastering Equivalent Fractions for Enhanced Mathematical Proficiency
Mastering the concept of equivalent fractions is a cornerstone of mathematical understanding. The ability to identify and work with equivalent fractions is crucial for success in algebra, geometry, and numerous other advanced mathematical concepts. Through understanding the principles of multiplication, division, simplification, and ratios, you can confidently navigate the world of fractions and their diverse applications. This guide has provided a comprehensive overview of the methods and applications involved in finding fractions equal to 2/5, equipped to tackle similar problems with confidence and skill. Remember to practice regularly, solidify your understanding, and approach any mathematical challenge with a clear and methodical mindset.
Latest Posts
Latest Posts
-
How Many Months Until Fall 2024
May 11, 2025
-
9 Oz Is How Many Cups
May 11, 2025
-
Cuanto Es 84 Pulgadas En Pie
May 11, 2025
-
How Many Cups In 58 Ounces
May 11, 2025
-
How Much Is 2 To 3 Ounces
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Fractions Are Equal To 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.