What Fractions Are Equivalent To 2/5
Treneri
May 14, 2025 · 6 min read
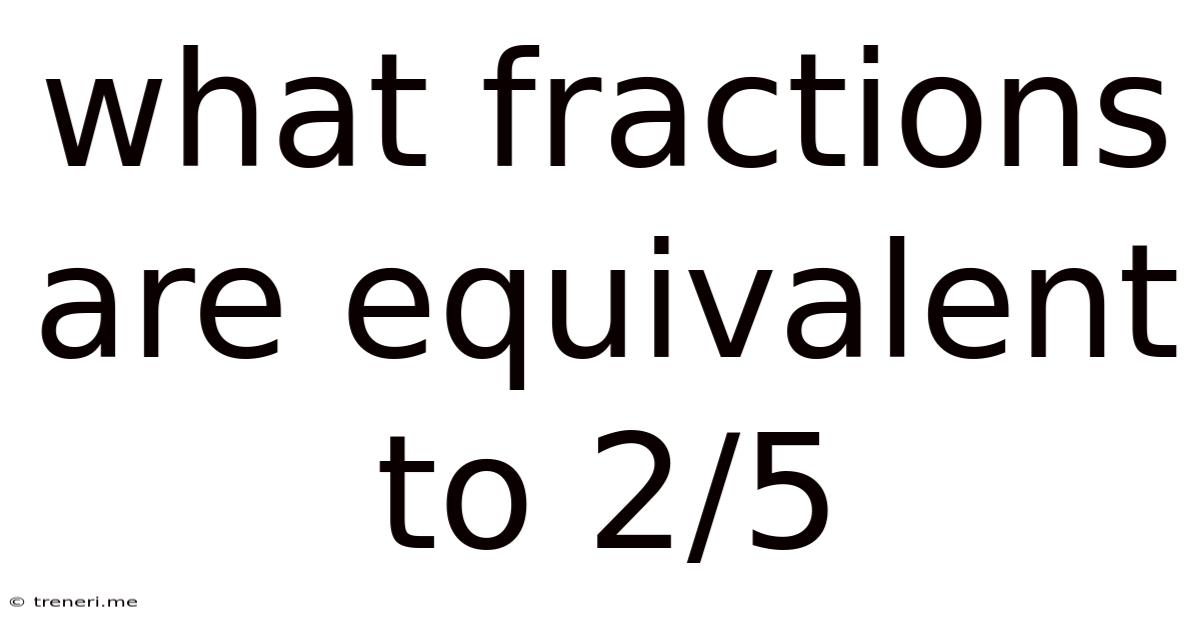
Table of Contents
What Fractions Are Equivalent to 2/5? A Comprehensive Guide
Understanding equivalent fractions is a fundamental concept in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This comprehensive guide delves into the intricacies of finding fractions equivalent to 2/5, exploring different methods, providing numerous examples, and highlighting the underlying principles. We'll also discuss the practical applications of this knowledge and offer tips for mastering this essential skill.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or part of a whole, even though they appear different numerically. They share the same value when simplified to their lowest terms. Think of it like slicing a pizza: one-half (1/2) is the same as two-quarters (2/4) or four-eighths (4/8). They all represent half of the pizza. The key to finding equivalent fractions is to multiply or divide both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number. This process maintains the ratio and thus the value of the fraction.
Methods for Finding Equivalent Fractions of 2/5
Several approaches can be used to determine fractions equivalent to 2/5. Let's explore the most common methods:
1. Multiplication Method
This is the most straightforward method. Simply multiply both the numerator (2) and the denominator (5) by the same integer (any whole number greater than zero).
- Multiplying by 2: (2 x 2) / (5 x 2) = 4/10
- Multiplying by 3: (2 x 3) / (5 x 3) = 6/15
- Multiplying by 4: (2 x 4) / (5 x 4) = 8/20
- Multiplying by 5: (2 x 5) / (5 x 5) = 10/25
- Multiplying by 10: (2 x 10) / (5 x 10) = 20/50
- Multiplying by 100: (2 x 100) / (5 x 100) = 200/500
This method generates an infinite number of equivalent fractions because you can multiply by any whole number.
2. Division Method (Simplification)
While the multiplication method creates equivalent fractions with larger numerators and denominators, the division method, also known as simplification, reduces the fraction to its lowest terms or finds equivalent fractions with smaller numerators and denominators. However, in the case of 2/5, it's already in its simplest form because 2 and 5 share no common factors other than 1. To illustrate, let's consider a fraction that is equivalent to 2/5, such as 4/10. Dividing both the numerator and denominator by their greatest common divisor (GCD), which is 2, we get: (4 ÷ 2) / (10 ÷ 2) = 2/5.
3. Using a Common Multiplier
This method is particularly useful when you need to find an equivalent fraction with a specific denominator. For example, if you need a fraction equivalent to 2/5 with a denominator of 25, you'd determine the multiplier by dividing the desired denominator (25) by the original denominator (5): 25 ÷ 5 = 5. Then, multiply both the numerator and denominator by this multiplier: (2 x 5) / (5 x 5) = 10/25. This method is helpful in comparing fractions with different denominators, a crucial skill in addition and subtraction of fractions.
Visual Representation of Equivalent Fractions
Visual aids can significantly enhance understanding. Consider representing 2/5 using shapes or diagrams. Divide a shape (a rectangle, circle, or square) into 5 equal parts and shade 2 of them. Now, consider dividing the same shape into 10 equal parts (double the original number of parts). You'll find that shading 4 of these 10 parts represents the same area as shading 2 out of 5 parts – visually confirming that 2/5 and 4/10 are equivalent. You can extend this visualization to other equivalent fractions such as 6/15, 8/20, and so on.
Practical Applications of Equivalent Fractions
Understanding and working with equivalent fractions is crucial in various real-world scenarios:
- Cooking and Baking: Recipes often require adjustments. If a recipe calls for 2/5 of a cup of sugar and you want to double the recipe, you need to find an equivalent fraction of 2/5 that represents double the amount (4/10 or 2/5 x 2 = 4/10).
- Measurement and Conversion: Converting between different units often involves working with equivalent fractions. For example, converting inches to feet or centimeters to meters.
- Finance and Budgeting: Calculating proportions of income, expenses, or investments relies heavily on understanding and manipulating equivalent fractions.
- Geometry and Mensuration: Calculating areas, volumes, and proportions of geometric shapes requires a solid grasp of fractions and their equivalents.
- Data Analysis and Statistics: Representing and interpreting data, especially proportions and percentages, necessitates a firm understanding of equivalent fractions.
Common Mistakes to Avoid
While working with equivalent fractions, certain mistakes are frequently encountered:
- Multiplying or Dividing Only the Numerator or Denominator: Remember, to maintain equivalence, both the numerator and denominator must be multiplied or divided by the same non-zero number.
- Incorrect Simplification: When simplifying fractions, ensure you divide both the numerator and the denominator by their greatest common divisor (GCD). Failing to do so leaves the fraction in a non-simplified form.
- Forgetting the Importance of the Whole: Always remember that fractions represent parts of a whole. This perspective helps in correctly interpreting and manipulating fractions.
Mastering Equivalent Fractions: Tips and Practice
Developing proficiency in working with equivalent fractions requires consistent practice and attention to detail. Here are some helpful tips:
- Start with Simple Fractions: Begin by practicing with easy fractions before moving to more complex ones.
- Use Visual Aids: Employ diagrams and shapes to visualize fractions and their equivalents. This approach enhances understanding and retention.
- Practice Regularly: Consistent practice strengthens your understanding of the concepts and builds your skills. Work through numerous problems to solidify your understanding.
- Utilize Online Resources: Many online resources, including interactive exercises and games, are available to aid in learning and practicing equivalent fractions.
- Seek Help When Needed: Don't hesitate to seek help from teachers, tutors, or online communities if you encounter difficulties.
Conclusion
Understanding and manipulating equivalent fractions is a fundamental skill with wide-ranging applications. By mastering the methods discussed in this guide, practicing regularly, and avoiding common pitfalls, you can develop a strong grasp of this essential mathematical concept. Remember, the key is consistent practice and a clear understanding of the underlying principles—that multiplying or dividing both the numerator and denominator by the same non-zero number preserves the value of the fraction. With dedication and practice, you'll find working with equivalent fractions becomes intuitive and straightforward. The numerous examples and practical applications illustrated in this guide should provide a strong foundation for further exploration and mastery of this crucial topic. Remember to always check your work and ensure your answers are simplified to their lowest terms. Happy fractioning!
Latest Posts
Latest Posts
-
How Many Days Is 366 Hours
May 15, 2025
-
What Year Is 35 Years Ago
May 15, 2025
-
An Inch Is What Fraction Of A Yard
May 15, 2025
-
How Many People Does 5 Lbs Of Mashed Potatoes Feed
May 15, 2025
-
How Much Is 550 Ml Of Water In Cups
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.