What Fractions Are Equivalent To 3/9
Treneri
May 10, 2025 · 5 min read
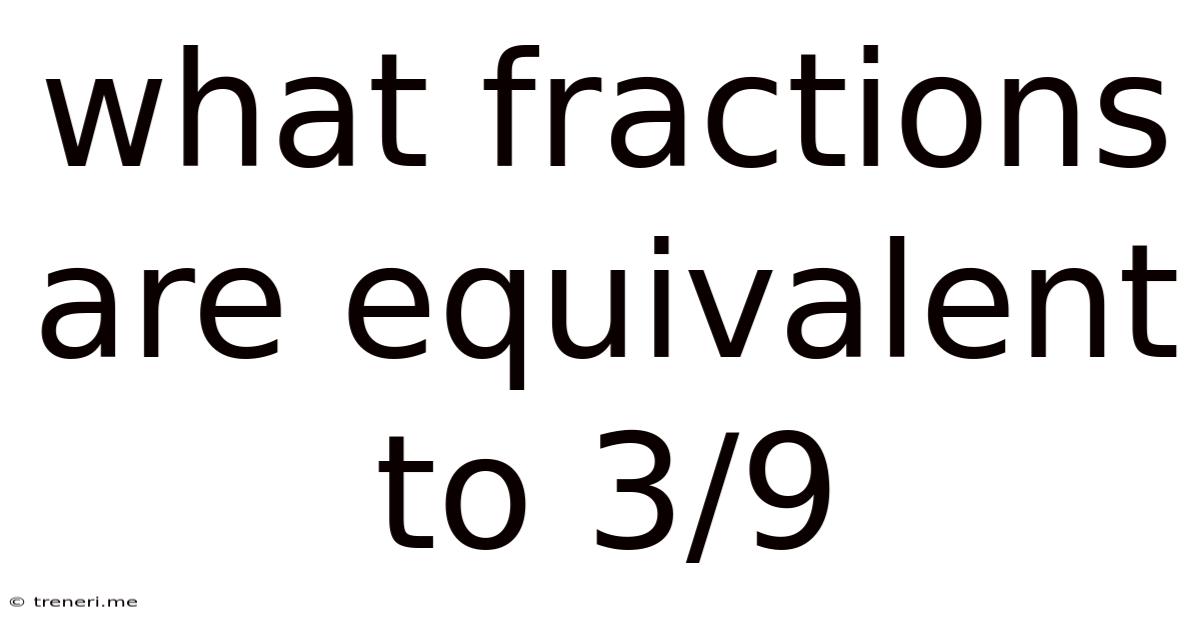
Table of Contents
What Fractions Are Equivalent to 3/9? A Comprehensive Guide
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding fractions, simplifying expressions, and solving various mathematical problems. This comprehensive guide will explore the concept of equivalent fractions, focusing specifically on fractions equivalent to 3/9. We'll delve into the methods for finding these equivalents, explore their applications, and address common misconceptions.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. Think of it like slicing a pizza: If you cut a pizza into 6 slices and take 2, it's the same as cutting the same pizza into 12 slices and taking 4. Both represent one-third of the pizza. Mathematically, this is represented as 2/6 = 4/12 = 1/3.
The key to understanding equivalent fractions lies in the concept of simplifying fractions. This involves reducing a fraction to its simplest form by dividing both the numerator (top number) and the denominator (bottom number) by their greatest common divisor (GCD).
Finding Equivalent Fractions to 3/9
The fraction 3/9 represents three parts out of nine equal parts. To find equivalent fractions, we need to multiply or divide both the numerator and the denominator by the same number (excluding zero). This doesn't change the overall value of the fraction; it merely changes its representation.
Method 1: Multiplying the Numerator and Denominator
We can create equivalent fractions to 3/9 by multiplying both the numerator and the denominator by the same whole number. Let's try a few examples:
- Multiply by 2: (3 x 2) / (9 x 2) = 6/18
- Multiply by 3: (3 x 3) / (9 x 3) = 9/27
- Multiply by 4: (3 x 4) / (9 x 4) = 12/36
- Multiply by 5: (3 x 5) / (9 x 5) = 15/45
- Multiply by 10: (3 x 10) / (9 x 10) = 30/90
As you can see, 6/18, 9/27, 12/36, 15/45, 30/90, and countless others are all equivalent to 3/9. This process can be repeated indefinitely, generating an infinite number of equivalent fractions.
Method 2: Simplifying the Fraction (Finding the Simplest Form)
While we can create many equivalent fractions by multiplication, it's often useful to simplify a fraction to its simplest form. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
The GCD of 3 and 9 is 3. Therefore, we can simplify 3/9 by dividing both the numerator and the denominator by 3:
3 ÷ 3 / 9 ÷ 3 = 1/3
Therefore, the simplest form of 3/9 is 1/3. This means that 1/3 is also an equivalent fraction to 3/9.
Visual Representation of Equivalent Fractions
Visual aids can significantly improve understanding. Imagine a rectangular shape divided into nine equal parts. Shading three of these parts visually represents 3/9. Now, imagine the same rectangle divided into three equal parts. Shading one of these parts represents 1/3. Both representations cover the same area, demonstrating the equivalence of 3/9 and 1/3. You can use similar visual representations with other equivalent fractions like 6/18 or 12/36 to reinforce the concept.
Applications of Equivalent Fractions
Understanding equivalent fractions is essential in many areas of mathematics and beyond:
-
Adding and Subtracting Fractions: Before adding or subtracting fractions, you often need to find equivalent fractions with a common denominator. For example, to add 1/3 and 1/6, you might convert 1/3 to its equivalent fraction 2/6.
-
Comparing Fractions: Determining which fraction is larger or smaller often requires converting them to equivalent fractions with a common denominator.
-
Ratio and Proportion: Equivalent fractions are fundamental to understanding ratios and proportions. A ratio of 3:9 is equivalent to the ratio of 1:3.
-
Real-World Applications: Equivalent fractions appear in numerous real-world situations, such as dividing recipes, measuring ingredients, and calculating percentages. For example, if a recipe calls for 3/9 of a cup of sugar, you can easily substitute 1/3 of a cup.
Common Misconceptions about Equivalent Fractions
-
Only multiplying or dividing by the GCD: While simplifying requires dividing by the GCD, finding equivalent fractions involves multiplying or dividing by any common factor, not just the GCD.
-
Changing the value of the fraction: Multiplying or dividing both the numerator and the denominator by the same number does not change the value of the fraction; it only changes its representation.
-
Limited number of equivalent fractions: There are infinitely many equivalent fractions for any given fraction, except for 0/1 (or any fraction equal to zero).
Practice Problems
To solidify your understanding, try finding equivalent fractions for 3/9:
- Find three equivalent fractions by multiplying the numerator and denominator.
- Find the simplest form of 3/9.
- Determine if 18/54 is an equivalent fraction to 3/9. Show your work.
- Explain why 3/10 is not an equivalent fraction to 3/9.
Conclusion
Equivalent fractions are a cornerstone of fractional arithmetic. Mastering the concepts of simplifying and generating equivalent fractions is vital for success in mathematics. Remember the simple rule: multiplying or dividing both the numerator and denominator by the same number (excluding zero) creates an equivalent fraction. Through practice and visual aids, you can solidify your understanding and confidently navigate the world of fractions. By understanding the principles outlined in this guide, you'll be well-equipped to solve various mathematical problems and apply these concepts in various real-world scenarios. The ability to identify and work with equivalent fractions will significantly enhance your mathematical skills and problem-solving abilities. Remember to practice regularly and utilize different methods to reinforce your understanding. The more you work with equivalent fractions, the more intuitive the concept will become.
Latest Posts
Latest Posts
-
Under 2 Hours Half Marathon Pace
May 10, 2025
-
How Many Cbm Is A 40ft Container
May 10, 2025
-
How Long To Hike 12 Miles
May 10, 2025
-
How Many Square Feet Does A Gallon Of Stain Cover
May 10, 2025
-
How Old Are 1995 Babies In 2024
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 3/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.